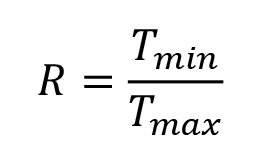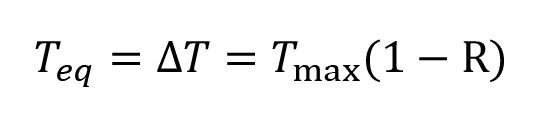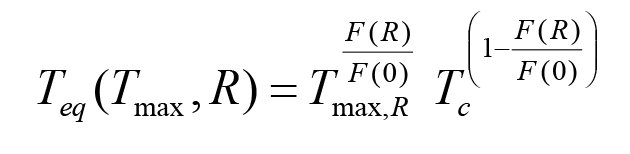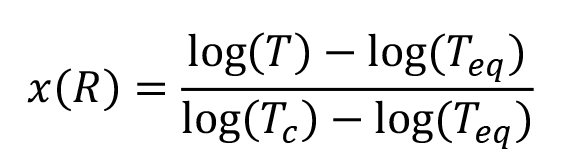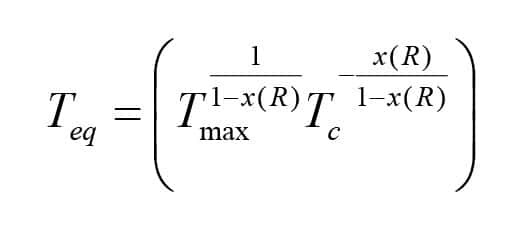Endurica CL and fe-safe/Rubber provide several material models for defining cyclic crack growth under nonrelaxing conditions. Nonrelaxing cycles occur when the ratio R is greater than zero. R is defined as
where T is the energy release rate (note that T will always be greater than or equal to zero).
The crack growth rate under nonrelaxing conditions is, in general, a function of both Tmax and R. For purposes of calculation, it is convenient to define an “equivalent” energy release rate Teq that gives the same steady state rate of crack growth as the operating condition on the nonrelaxing crack growth curve, but which is instead on the fully relaxing crack growth curve. In other words,
Using this scheme, you can set up models for both amorphous and strain-crystallizing rubbers, depending on your definition of Teq. Amorphous rubbers follow the well-known Paris model, and strain-crystallizing rubbers follow the Mars-Fatemi model (or you can define a lookup table).
Paris Model (Amorphous):
The Paris model is the simplest to derive, as it does not involve any material parameters. It defines the equivalent energy release rate as
This definition is only suitable for rubbers that do not strain-crystallize.
For strain-crystallizing rubbers, one of the other two models should be used.
Mars-Fatemi Model (Strain-crystallizing):
The Mars-Fatemi model accounts for strain crystallization by treating the power-law slope, F, of the Thomas fatigue crack growth rate law ![]() as a function of R, where
as a function of R, where
or
The exponential version is more compact, but the polynomial version is more flexible.
By substituting F(R) into the fatigue crack growth rate equations for relaxing and nonrelaxing cases, and doing a bit of algebra, the following relationship is obtained
Lookup Table (Strain-crystallizing):
The most flexible and accurate way to define strain crystallization is via a lookup table. The lookup table takes R as an input and returns x(R) as an output. This function can be defined as the fraction x(R) by which the nonrelaxing crack growth curve is shifted between the fully relaxing crack growth curve (x=0), and the vertical asymptote at Tc (x=1), at a given R.
This can be rearranged into the desired Teq (Tmax,R) form, as follows
Comparisons:
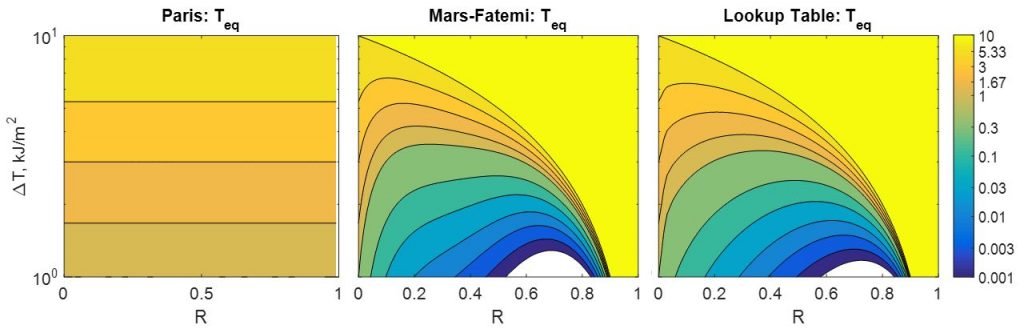
Visualizing the differences between the models helps gain a better understanding of how strain crystallization can affect fatigue performance. Since all of these models can be represented in the same form of Teq(Tmax,R), we show 2-D contour plots of Teq with R on the x-axis and ∆T on the y-axis. ∆T is used instead of Tmax to make it easier to compare back to the simple Paris model.
From the figures above, we see that for the Paris model, the equivalent energy release rate depends only on ∆T. When using this model, changes in R will have no effect on fatigue performance (when ∆T is also held constant).
For strain-crystallizing rubbers, changes in R should influence fatigue performance. This is seen in the figures for the Mars-Fatemi and lookup table models.
The Mars-Fatemi example uses the following parameters:
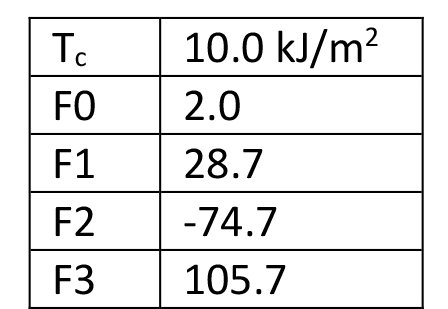
The lookup table example uses Tc=10.0 kJ/m2 and Lindley’s data for unfilled natural rubber (P. B. Lindley, Int. J. Fracture 9, 449 (1973)).
For these models, there is a significant decline in Teq as R increases. This effect is most pronounced when Tmax is much smaller than the critical energy release rate Tc. Also, there is a point where the effect is reversed (around R=0.8 in these examples) and the high R-ratio starts to have a negative effect on fatigue performance.
Implications:
A material’s strain crystallization properties’ impact on fatigue performance under non-relaxing conditions should not be ignored. Whether you are seeking to take advantage of strain-crystallization effects or simply comparing the results of different materials/geometries/loadings, strain-crystallization should be accurately represented in your simulations.
Follow these tips to take advantage of strain crystallization and help ensure your fatigue performance is the best it can be.
- Take advantage of Endurica’s material characterization service (the FPM-NR Nonrelaxing Module generates the strain crystallization curve) or use your own in-house testing to create an accurate strain crystallization model of your material (the nonrelaxing procedure is available for the Coesfeld Tear and Fatigue Analyser).
- Use output requests like DAMAGE_SPHERE, CEDMINMAX and CEDRAINFLOW to observe R-ratios for your duty cycles.
References
- B. Lindley, Int. J. Fracture 9, 449 (1973)
Mars, W. V. “Fatigue life prediction for elastomeric structures.” Rubber chemistry and technology 80, no. 3 (2007): 481-503.
Mars, W. V. “Computed dependence of rubber’s fatigue behavior on strain crystallization.” Rubber Chemistry and Technology 82, no. 1 (2009): 51-61.
Barbash, Kevin P., and William V. Mars. Critical Plane Analysis of Rubber Bushing Durability under Road Loads. No. 2016-01-0393. SAE Technical Paper, 2016.