Discover how industry leaders are transforming their durability programs by simulating real-world road loads for rubber parts. This webinar features a verification and validation project... Continue reading
- We Offer
Elastomer Durability Analysis Solutions
Discover the Science Behind Elastomer Fatigue
Take your designs to the next level with models tailored specifically for rubber materials.
- Industry Solutions
- Resources
- About
- Contact
Rubber durability isn’t just a detail — it’s the difference between success and failure — especially in the rail industry. That’s why Endurica’s Winning on... Continue reading
Rubber durability isn’t just a detail — it’s the difference between success and failure — especially in the rail industry. That’s why Endurica’s Winning on... Continue reading
It was May of 2023, and Will Mars had just given a presentation on “Virtual Qualification of the Durability Performance of an Elastomeric Mount with... Continue reading
All materials are temperature dependent, but some more than others: metals tend to be crystalline solids and will melt at sufficiently high temperatures; in contrast,... Continue reading
Wow – this year has really been one of many firsts for Endurica. We had our first ever Community Conference in April, we started our... Continue reading
The load cases to be considered in fatigue analysis can be very lengthy and can involve multiple load axes. Often, load cases are much longer... Continue reading
Rubber and metal are very different materials that exhibit very different behaviors. Consider the effect of mean strain or stress on the fatigue performance of... Continue reading
There were several papers on fatigue life prediction for elastomers at SAE WCX 2022, but the highlight for us was this one from Automotive... Continue reading
Ever wonder what it takes to consistently deliver quality and reliability in our software releases? Here’s a brief overview of the systems and disciplines we... Continue reading
Showing 1–10 of 11 posts
Recent Posts
- Multi-Year Maintenance & Support Bundles for Perpetual License Holders
- Engineering Failure Analysis — published in affiliation with European Structural Integrity Society
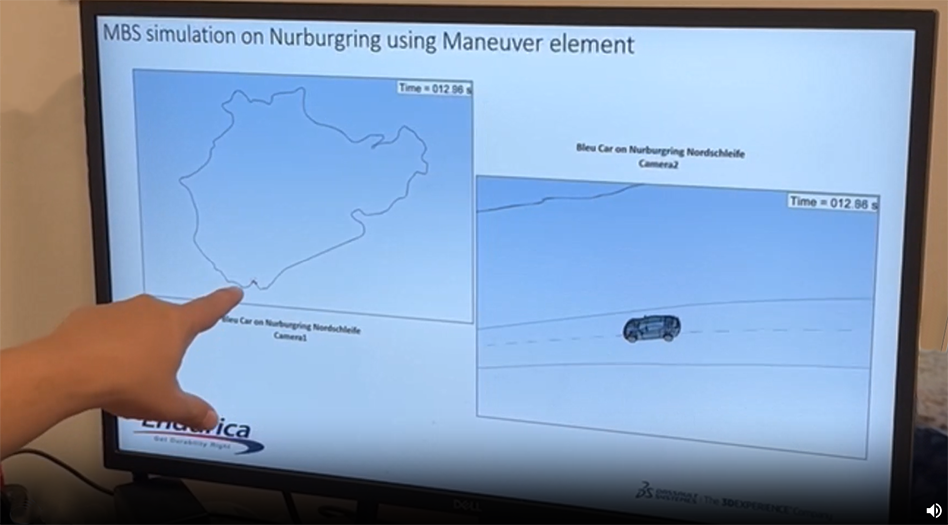
- Taming the Tarmac: Simulating Tire Durability on the Nürburgring
- Rubber Fatigue ≠ Metal Fatigue Part 3: Thermal Effects
- 4-in-1: Community Conference
Categories
No comments to show.
© 2025 Copyright Endurica LLC
Website Designer iGo Sales and Marketing, Inc.