Endurica is committed to building long-term, strategic relationships that support our clients’ success well beyond the initial purchase of a software license. In response to... Continue reading
- We Offer
Elastomer Durability Analysis Solutions
Discover the Science Behind Elastomer Fatigue
Take your designs to the next level with models tailored specifically for rubber materials.
- Industry Solutions
- Resources
- About
- Contact
William V. Mars, Ph.D., P.E. is a co-author of the article A Preliminary Conceptual Study for Coupled Thermo-Mechanical and Structural Characterization of Rim-Supported Run-Flat Tires which... Continue reading
It was May of 2023, and Will Mars had just given a presentation on “Virtual Qualification of the Durability Performance of an Elastomeric Mount with... Continue reading
All materials are temperature dependent, but some more than others: metals tend to be crystalline solids and will melt at sufficiently high temperatures; in contrast,... Continue reading
Wow – this year has really been one of many firsts for Endurica. We had our first ever Community Conference in April, we started our... Continue reading
The load cases to be considered in fatigue analysis can be very lengthy and can involve multiple load axes. Often, load cases are much longer... Continue reading
Rubber and metal are very different materials that exhibit very different behaviors. Consider the effect of mean strain or stress on the fatigue performance of... Continue reading
2023 marked year 15 for Endurica. If I had to pick one word to describe the past year, that word would be “vector”. Because magnitude... Continue reading
When there is rolling or sliding contact of a rubber surface over a second hard surface of sufficient roughness, localized cutting and damage of the... Continue reading
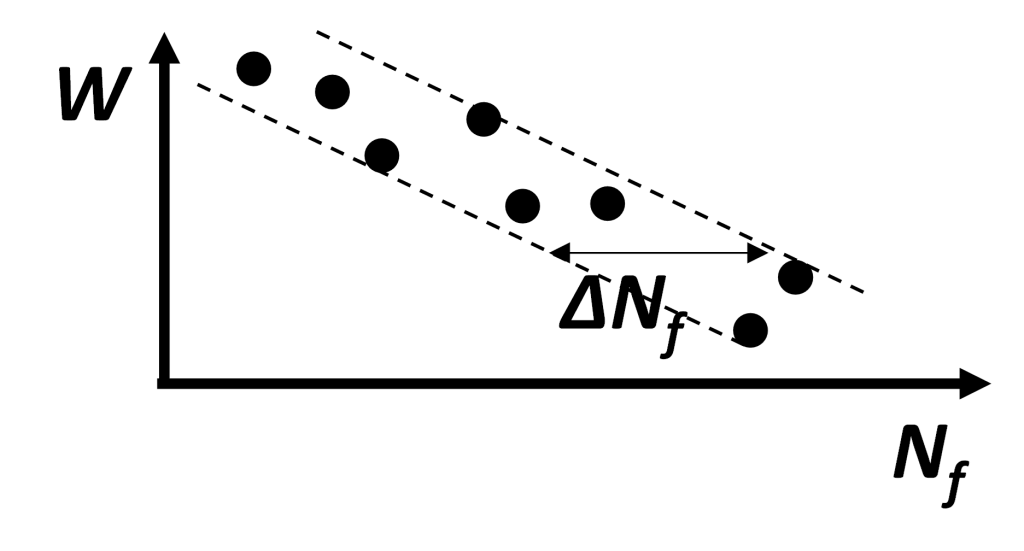
I get this question a lot: how well can the Endurica software predict fatigue life? Is it as good as a metal fatigue code, where... Continue reading
Showing 1–10 of 51 posts
Recent Posts
- Multi-Year Maintenance & Support Bundles for Perpetual License Holders
- Engineering Failure Analysis — published in affiliation with European Structural Integrity Society
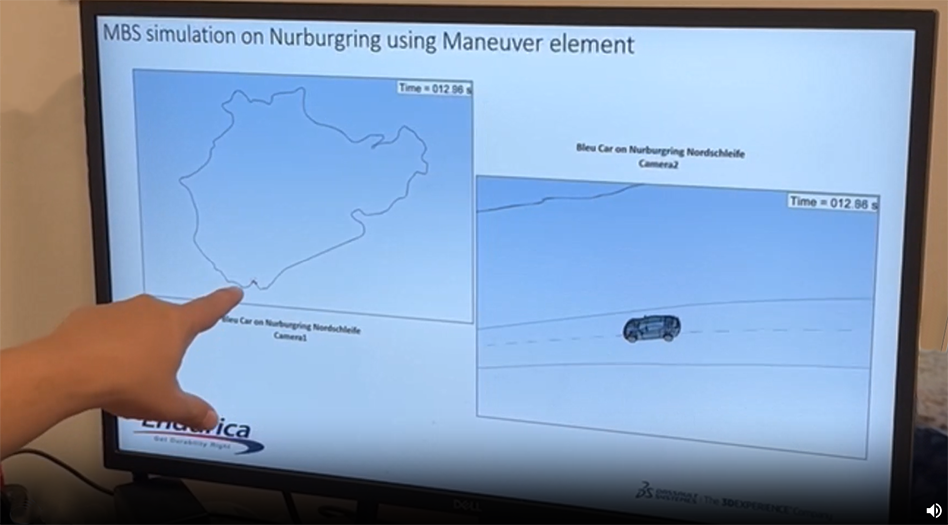
- Taming the Tarmac: Simulating Tire Durability on the Nürburgring
- Rubber Fatigue ≠ Metal Fatigue Part 3: Thermal Effects
- 4-in-1: Community Conference
Categories
No comments to show.
© 2025 Copyright Endurica LLC
Website Designer iGo Sales and Marketing, Inc.