It was May of 2023, and Will Mars had just given a presentation on “Virtual Qualification of the Durability Performance of an Elastomeric Mount with... Continue reading
- We Offer
Elastomer Durability Analysis Solutions
Discover the Science Behind Elastomer Fatigue
Take your designs to the next level with models tailored specifically for rubber materials.
- Industry Solutions
- Resources
- About
- Contact
All materials are temperature dependent, but some more than others: metals tend to be crystalline solids and will melt at sufficiently high temperatures; in contrast,... Continue reading
Wow – this year has really been one of many firsts for Endurica. We had our first ever Community Conference in April, we started our... Continue reading
The load cases to be considered in fatigue analysis can be very lengthy and can involve multiple load axes. Often, load cases are much longer... Continue reading
Rubber and metal are very different materials that exhibit very different behaviors. Consider the effect of mean strain or stress on the fatigue performance of... Continue reading
2023 marked year 15 for Endurica. If I had to pick one word to describe the past year, that word would be “vector”. Because magnitude... Continue reading
Overview The accuracy of the interpolated results performed by EIE is dependent on the discretization of the map. Specifically, the results will become more accurate... Continue reading
Endurica CL and fe-safe/Rubber provide several material models for defining cyclic crack growth under nonrelaxing conditions. Nonrelaxing cycles occur when the ratio R is greater... Continue reading
The relationship between crack nucleation and fracture mechanics experiments for polymers was first documented in 1964 by Gent, Lindley and Thomas (Journal of Applied Polymer... Continue reading
Recent Posts
- Multi-Year Maintenance & Support Bundles for Perpetual License Holders
- Engineering Failure Analysis — published in affiliation with European Structural Integrity Society
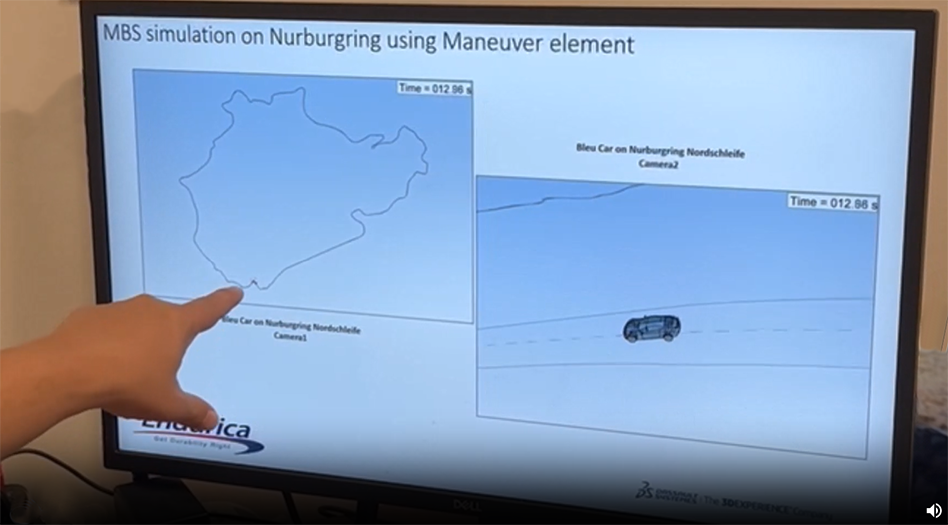
- Taming the Tarmac: Simulating Tire Durability on the Nürburgring
- Rubber Fatigue ≠ Metal Fatigue Part 3: Thermal Effects
- 4-in-1: Community Conference
Categories
No comments to show.
© 2025 Copyright Endurica LLC
Website Designer iGo Sales and Marketing, Inc.