Critical Plane Analysis

Rubber Fatigue ≠ Metal Fatigue Part 2: Linear Superposition

August 29, 2024August 28, 2024 by William V. Mars, Ph.D., P.E.

Rubber Fatigue DOES NOT EQUAL Metal Fatigue Part 2 Linear Superposition

The load cases to be considered in fatigue analysis can be very lengthy and can involve multiple load axes. Often, load cases are much longer than can be calculated via direct time-domain finite element analysis (FEA).

In metal fatigue analysis, linear superposition is a widely used technique to generate stress-strain history from road loads [1], [2], [3]. When structures behave linearly, this approach is accurate and computationally efficient, allowing the analysis of lengthy load signals. For single axis problems, the finite element (FE) solution for a single unit load case is simply scaled according to the input load history. For multiaxial problems, unit load cases are solved for each of the axes, then scaled and combined according to the input load history.

Due to rubber’s 1) nonlinear material behaviour, 2) nonlinear kinematics, and 3) the possibility of nonlinear contact, linear superposition cannot be applied to rubber fatigue analysis. This article is the second in a series examining how rubber fatigue analysis procedures differ from those used for metal fatigue. Here we present the Endurica EIE^TM (Endurica Interpolation Engine) solver, which is a tool for the rapid generation of stress-strain histories for fatigue analysis in cases where linear superposition fails.

Fig.1. Nonlinearity figures in the analysis of rubbery materials in several ways including material nonlinearity, kinematic nonlinearity, and contact linearity. Endurica’s EIE solver provides an efficient and accurate method for generating stress-strain history when there is strong nonlinearity.

Brief review of the linear superposition procedure for metals

For linear structures, the relationship between forces [F] and displacements [u] can be written as a matrix multiplication where [k] is the stiffness matrix.

[F] = [k][u]

The associative property of function composition means that multiplying the displacements by a scalar a produces proportionally larger forces.

a[F] = [k](a[u])

The distributive property of addition means that a force system resulting from combined displacements [u] and [v]

[F] = [k][u] +[k][v]

can also be calculated as

[F] = [k]([u] + [v])

Similarly, stress and strain fields can be scaled and combined by linear superposition. Engineers have been using this principle for many years in metal fatigue analysis, particularly for treating multiaxial cases arising from field-recorded load-displacement histories.

The stress and strain fields in a part are assumed to result from a linear combination of unit load cases, where the scale factor for each unit load case is applied to the stress or strain field corresponding to a given input channel.

For example, for the beam shown in Fig.2, if channel 1 is the unit displacement u with magnitude a(t), and channel 2 is another unit displacement v elsewhere in the structure with magnitude β(t) , then the entire history of stress and strain at all points in the beam can be recovered by linear superposition.

Note that the FE solver only needs to produce a single time-independent solution for each unit load case. The time dependence of the solution is obtained entirely through the time variations of the scale factors a(t) and β(t). This extremely efficient method has been used for many years in metal fatigue analysis. It allows rapid analysis of complete road load histories consisting of millions of time steps.

Fig.2. Linear superposition of single load case FE solutions has long been used to generate stress-strain histories from road load histories in metal fatigue analysis.

Endurica EIE^TM: load space discretization and interpolation for nonlinear cases

Solving the nonlinear case requires a completely different approach. We wish to retain the advantages of efficiently constructing stress-strain time histories from precomputed FE solutions. Instead of precomputing a single unit load case for each input channel, we precompute a set of load cases from a discretized load space. We call this set a map.

The number of load cases in the map must be sufficient so that we can use interpolation to obtain an reasonable approximation of the nonlinear response at any point within the map. Fig.3 shows a map with two channels defined by x and z displacements. The blue points in the map are precalculated using an FE solver such as Ansys or LS-Dyna following the path traced by the blue line. Once the map is defined, the stress-strain history along the red line can be interpolated from the precomputed solutions in the map.

Endurica EIE discretization map — Fig.3. Two-channel map discretizing a space defined by the x and z displacements. Blue dots represent FE solutions for which the stress-strain fields are precomputed. The blue line represents a solution path, which defines the order in which the solutions are computed and stored in the results database. The red line represents a possible actual displacement history. The stress-strain history for points on the red path is obtained by interpolation from points on the precomputed map.

Endurica EIE^TM is a general purpose tool for creating and using non-linear maps to generate stress-strain histories for fatigue analysis [4], [5]. EIE is an abbreviation for efficient interpolation engine. EIE provides a simple workflow and powerful utilities for creating and using maps for interpolation. It supports up to six independent input channels.

The entire EIE workflow consists of three main steps. The first step is to create a map. The next step is to specify your history in terms of forces or displacements. Note that any quantity that can be applied as a boundary condition to the FE model can be set up as a channel. The last step is to perform the specified interpolation. The process produces a time history of strain tensor components for each element in your FE model.

The map creation process involves four steps, as shown in Fig.4. First, the number of independent channels that will be used to specify the history must be defined. The map type must also be specified. Several types are available, including a completely customizable map. Grid-based maps are often appropriate for one-, two- and three-dimensional maps. For higher dimensional maps, case vector-based maps are often the most convenient.

Once the map type has been defined, EIE generates solution paths. These consist of enumerated load states that should be applied as boundary conditions to the FE model to generate the map. One or more paths may be generated depending on map type. Each path is called a branch. For each branch, EIE writes a file with the appropriate boundary condition history, which is necessary for the generation of the map. Next, the FE model is set up and executed using EIE’s boundary conditions. Finally, the database of FE results is linked to the corresponding branch in the definition of the map.

At this point the map is complete and ready for interpolation. Note that linear superposition can be implemented as a special case in EIE when unit load case solutions are collected and defined as a map. In general, however, a non-linear map will contain a greater number of solution steps.

Steps to specify a map for use by Endurica EIE. — Fig.4. Steps to specify a map for use by Endurica EIE^TM.

Specifying the load history is as simple as selecting a file containing the time history of each input channel. In the file, each row represents one time step and each column represents an input channel. EIE supports .csv and .rsp formats, both common data formats. Fig.5 shows an example history with and displacements. Note that the range of displacements in the history should not exceed the range of the precalculated map. Although interpolated solutions can be quite accurate, extrapolation for non-linear problems can be very risky and inaccurate.

Endurica example of two-channel displacement history for interpolation — Fig.5. Example two-channel displacement history for interpolation.

Once the map and history are specified, interpolation can begin. Endurica EIE^TM supports multi-threading, meaning that interpolation calculations can be distributed and executed in parallel across available CPUs. This makes interpolating very fast and very scalable to large models and lengthy histories. Note that Endurica EIE^TM generates large files because it calculates stress and strain tensor components for each time step of each finite element. It is therefore important to ensure that you have sufficient disk space available when running Endurica EIE^TM.

Comparing linear and non-linear interpolation results for a sway bar under uniaxial loading

As a first example, consider an automotive sway bar link, shown in Fig.7. The sway bar transmits load in a single axial direction. This model uses Ogden’s hyper elastic law, which involves a non-linear relationship between stress and strain. The large deformation solution also involves non-linear kinematics due to the incompressibility of rubber and finite displacements and rotations. To compare the linear and non-linear interpolation methods, we will run the analysis using both: 1) the linear scaling method (where the map consists of a single load case in which we apply one newton of total load in the x-direction to the link and solve for the strain distribution in the part); and 2) the non-linear method (where the map consists of 11 precomputed steps ranging from -10000N to +10000N).

Endurica sway bar analysis area noted by red arrows — Fig.6. Sway bar link under uniaxial loading (left). Axial load history input for strain history interpolation (right).

Figs. 8–10 show the six engineering strain tensor component history results for both the linear superposition procedure (left) and the nonlinear EIE procedure (right). The results are shown for three different locations on the sway bar bushing (highlighted in red). The largest strain component is the 31 shear (orange line). Note that for the linear procedure, a linear increase in the amplitude of the global force results in a linear increase in the strain components. The non-linear procedure produces quite different results. In fact, where the linear solution predicts symmetry of tension and compression loads, the non-linear solution correctly captures asymmetries.

Endurica Sway Bar Analysis linear and nonlinear — Fig.7. Comparison of linear (left) and non-linear (middle) interpolation results for strain tensor components at the location indicated on the right.

Enduria sway bar analysis top area — Fig.8. Comparison of linear (left) and non-linear (middle) interpolation results for strain tensor components at the location indicated on the right.

Endurica sway bar analysis top at edge — Fig.9. Comparison of linear (left) and non-linear (middle) interpolation results for strain tensor components at the location indicated on the right.

As a final comparison, Fig.11 shows the fatigue life calculated using Endurica CL^TM. A longer fatigue life is predicted for the non-linearly interpolated case compared to the linearly interpolated case. Note that the fatigue damage is more concentrated in the linear case and more spatially distributed for the non-linear solution.

Endurica sway bar analysis Linear versus Nonlinear — Fig.10. Comparison of fatigue life calculations based on linear (left) and non-linear (right) interpolated strain history.

Endurica EIE^TMvalidation for a six-channel non-linear interpolation

As a further test of the non-linear interpolation procedure for a six-channel ( forces + moments) multiaxial load analysis of the gearbox mount shown in Fig.11, the map shown in Fig.12 was defined. This map contained 51 precalculated non-linear FE solutions. The complete loading history to be interpolated is shown in Fig.13. This history was solved in full directly and interpolated from the map using Endurica EIE^TM.

Endurica Gearbox Mount Analysis — Fig.11. Gearbox mount analysis. All forces and moments (x, y, and z) were applied at the centre of the top rigid mounting plate.

Endurica Six-channel map containing 51 precalculated finite element solutions. — Fig.12. Six-channel map containing 51 precalculated finite element solutions.

Endurica Full six-channel road load history used for validation analysis of gearbox mount. — Fig.13. Full six-channel road load history used for validation analysis of gearbox mount.

The strain tensor histories for the 11, 22 and 12 strain components are compared between the directly solved and interpolated solutions in Fig.14 at the location of the most critical element. A fairly accurate interpolation was obtained with a much shorter run time than the direct finite element analysis of the full history.

Endurica Comparison of EIE-interpolated strain components (blue) v. direct finite element solution (red) at the location of the most critical element. — Fig.14. Comparison of EIE-interpolated strain components (blue) v. direct finite element solution (red) at the location of the most critical element.

The fatigue life of the gearbox mount was calculated with Endurica CL^TM using both the EIE-interpolated strain history and the directly solved strain history. The fatigue contours for both cases are shown in Fig.15. The fatigue life for the interpolated history was 7.52E8 and for the directly solve history the fatigue life was 7.87E8. These results indicate a close agreement between the EIE and directly solved cases. Other validation cases were recently published elsewhere (Mars et al 2024).

Endurica comparison of fatigue life calculated from EIE-interpolated strain components (right) and direct finite element solution (left). — Fig.15. Comparison of fatigue life calculated from EIE-interpolated strain components (right) and direct finite element solution (left).

Conclusion

Analysis of rubber components typically involves strong nonlinearities due to material behaviour, finite strain kinematics, and contact. The traditional linear superposition of unit load cases, widely used in metal fatigue analysis, is not effective in such cases. Fortunately, the Endurica EIE^TM solver can generate strain histories efficiently and accurately in these cases. The EIE tools allow the analysis to precalculate a set of FE solutions for efficient discretization of the load space and accurate interpolation of signals within the load space. With sufficient discretization of the load space, it was shown that quite accurate results can be produced for cases where there are between one and six load input channels.

References

[1.] R. W. Landgraf, “Applications of fatigue analyses: transportation”, Fatigue ’87, vol. 3, pp. 1593–1610, 1987

[2.] Moon, Seong-In et al, “Fatigue life evaluation of mechanical components using vibration fatigue analysis technique”, Journal of Mechanical Science and Technology, vol. 25, pp. 631–637, 2011.

[3.] F. A. Conle and C. W. Mousseau, “Using vehicle dynamics simulations and finite-element results to generate fatigue life contours for chassis components”, International Journal of Fatigue, vol. 13(3), pp. 195–205, 1991.

[4.] K. P. Barbash and W. V. Mars, “Critical plane analysis of rubber bushing durability under road loads”, SAE Technical Paper No. 2016-01-0393, 2016.

[5.] W. V. Mars, “Interpolation engine for analysis of time-varying load data signals”. U.S. Patent 9, 645, 041, May 9, 2017.

[6.] W. Mars, K. Barbash et al, “Durability of Elastomeric Bushings Computed from Track-Recorded Multi-Channel Road Load Input”, SAE Technical Paper No. 2024-01-2253, 2024.

Rubber Fatigue ≠ Metal Fatigue Part 1: Mean Strain Effects

April 24, 2024April 19, 2024 by William V. Mars, Ph.D., P.E.

Rubber Fatigue does not equal Metal Fatigue Part 1 Mean Strain Effects

Figure 1. Constant amplitude cycles at three different mean strains.

Rubber and metal are very different materials that exhibit very different behaviors. Consider the effect of mean strain or stress on the fatigue performance of these materials. Figure 1 illustrates a few typical constant amplitude strain cycles, each at a different level of mean strain. If the stress amplitude is equal to the mean stress, we say that we have pulsating tension or fully relaxing tension. If the mean stress is zero, we say that we have fully reversed tension/compression. If the minimum stress is always positive, then we have nonrelaxing tension (i.e. always under load). Nonrelaxing cycles are quite common in applications. Examples include: pre-loads applied during installation; swaging of a bushing to induce compressive pre-stresses, interference fits, self-stresses occurring due to thermal expansion/contraction; and in tires, shape-memory effects of textile cords.

In metal fatigue analysis, it is customary to define the effect in terms of stress amplitude σ_a and mean stress σ_m, relative to the yield stress σ_y and the ultimate stress σ_u, as shown in Figure 2. Below the fatigue threshold stress σ₀, indefinite life is predicted. The Haigh (or Goodman)

Figure 2. Haigh diagram (left) and Wohler curves (right) showing mean strain effects on fatigue life for a metal.

diagram (left) maps fatigue life as a function of these parameters [1]. Wohler curves (right) provide similar information. For metals, a simple rule may be applied universally: increasing mean strain is detrimental fatigue life. It is also commonly assumed for metals that the critical plane is perpendicular to maximum principal stress direction.

There are many ways that rubber materials differ from metallic materials. At the atomic scale, rubber is composed of long chain molecules experiencing constant thermal motion while interlinked with a permanent network topology. This structure permits large, elastic/reversible straining to occur. Metals could not be more different, existing as individual atoms packed into well-ordered crystals with occasional dislocations or lattice vacancies. This structure permits only vanishingly small strains before inelastic deformation occurs. At the meso scale, rubber is typically a composite material containing fillers such as carbon black, silica or clay, as well as other chemical agents. The mesoscale of a metal is generally described in terms of crystalline grain boundaries and inclusions or voids. Rubber exhibits many “special effects” that are not seen in metals: rate and temperature dependence, ageing, cyclic softening. It is unsurprising that analysis methods for rubber differ substantially from those applied for metals.

Rubber’s fatigue performance has a more complex dependence on mean strain. For amorphous (ie non-crystallizing) rubbers, increasing mean strain reduces the fatigue life, as with metals. But for rubbers that exhibit strain-induced crystallization, mean strain can greatly increase fatigue life, as illustrated in Figure 3. Fatigue simulations therefore must take account of the strain crystallization effect.

Figure 3. Fatigue tests run in simple tension under constant amplitude show a significant increase in life for Natural Rubber (NR), which strain crystallizes, and a decrease of life for Styrene Butadiene Rubber (SBR) which is amorphous [2].

Mean strain effects are specified in the Endurica fatigue code in terms of fracture mechanical behavior, using the concept of an equivalent fully relaxing tearing energy T_eq. The tearing energy for fully relaxing conditions is said to be equivalent when it produces the same rate of crack growth as the nonrelaxing condition. For amorphous rubbers, the equivalent R=0 tearing energy T_eq is simply the range ΔT of the tearing energy cycle, which can be expressed in terms of the min and max tearing energies T_min and T_max, or in terms of R= T_min / T_max. Plugging this rule into the power law crack growth rate function yields the well known Paris law, which predicts faster crack growth for increasing mean strain. For a strain crystallizing rubber, the equivalent fully relaxing tearing energy can be specified using the Mars-Fatemi law. In this case, the equivalent fully relaxing tearing energy depends on a function F(R), which specifies the crystallization effect in terms of its influence on the powerlaw slope of the crack growth rate law. The relationship for amorphous and crystallizing rubbers are summarized in Table 1 [3,4].

Table 1. Models for computing crack growth rate in amorphous and strain-crystallizing rubbers.

Rubber’s fatigue behavior may be plotted in a Haigh diagram, but the contours can be quite different than for metals. In metal fatigue analysis, it is assumed that cracks always develop perpendicular to the max principal stress direction. This is not always true for rubber, especially in cases involving strain crystallization and nonrelaxing loads. For rubber fatigue analysis it is therefore required to use critical plane analysis [5], in which fatigue life is computed for many potential crack orientations, and in which the crack plane with the shortest life is identified as the most critical plane. Figure 4 shows the dependence of the fatigue life and the critical plane orientation on strain amplitude and mean strain. A sphere is plotted for each pair of strain amplitude and mean strain coordinates, on which the colors represent fatigue life, and unit normal vectors indicate critical plane orientations. It can be seen that different combinations of mean strain and strain amplitude can produce a range of crack plane orientations.

Figure 4. Critical plane analysis consists in integrating the crack growth rate law for every possible crack orientation, and identifying the orientation that produces the shortest life (left). Each point in the Haigh diagram (right) is associated with its own critical plane orientation.

The Haigh diagrams for natural rubber (NR) and for styrene butadiene rubber (SBR) are shown in Figure 5. In these images, red represents short fatigue life, and blue long life. For natural rubber (on the left), the long-life region of the Haigh diagram exhibits a notable dome-like shape, indicative of a beneficial effect of mean strain under the influence of strain-induced crystallization. In contrast, SBR always exhibits decreased fatigue life as mean strain increases. Even so, the Haigh diagram for SBR has a nonlinear character associated with the material’s hyperelasticity that is also distinct from a metal.

Figure 5. Haigh diagrams computed for NR (left) and for SBR (right) rubbers.

It should be noted that the strain crystallization effect in rubber depends on temperature. At colder temperatures, the effect is stronger, and at higher temperatures it is weaker. Figure 6 compares experimental Haigh diagrams [6] (top) for a crystallizing rubber to computed results (bottom) for three temperatures.

Figure 6. Experimental Haigh diagram [6] for natural rubber at 3 temperatures (top), compared to computed Haigh diagram (bottom). Increasing temperature tends to reduce the beneficial effect of strain crystallization.

In summary, while tensile mean stresses are always detrimental in metals, in rubber they may be either beneficial or harmful, depending on whether the rubber can strain crystallize. The benefits of mean stresses in rubber can be quite strong – sometimes amounting to more than several orders of magnitude. The beneficial effect is stronger at colder temperatures and is reduced at higher temperatures. Critical Plane Analysis is essential for accurately predicting the effects of strain crystallization in rubber. Wohler curves, commonly used for metal fatigue analysis, incorrectly assume that the worst-case plane is always normal to the max principal stress direction. This is not an accurate approach for strain crystallizing rubber under mean strain. Use the Endurica fatigue solvers to accurately capture these effects when its important to get durability right!

References

[1] Stephens, R. I., Fatemi, A., Stephens, R. R., & Fuchs, H. O. (2000). Metal fatigue in engineering. John Wiley & Sons.

[2] Ramachandran, Anantharaman, Ross P. Wietharn, Sunil I. Mathew, W. V. Mars, and M. A. Bauman. (2017) “Critical plane selection under nonrelaxing simple tension with strain crystallization.” In Fall 192nd technical meeting of the ACS Rubber Division, pp. 10-12.

[3] Mars, W. V. (2009). Computed dependence of rubber’s fatigue behavior on strain crystallization. Rubber Chemistry and Technology, 82(1), 51-61.

[4] Harbour, Ryan J., Ali Fatemi, and Will V. Mars. “Fatigue crack growth of filled rubber under constant and variable amplitude loading conditions.” Fatigue & Fracture of Engineering Materials & Structures 30, no. 7 (2007): 640-652.

[5] Mars, W. V. (2021). Critical Plane Analysis of Rubber. Fatigue Crack Growth in Rubber Materials: Experiments and Modelling, 85-107.

[6] Ruellan, Benoît, J-B. Le Cam, I. Jeanneau, F. Canévet, F. Mortier, and Eric Robin. “Fatigue of natural rubber under different temperatures.” International Journal of Fatigue 124 (2019): 544-557.

Tension / Compression Cycles, R ratio and a Discussion of Wohler Curve for Rubber

May 24, 2022April 22, 2022 by William V. Mars, Ph.D., P.E.

Fatigue Life of Rubber with different strain constraints

In fatigue testing, R is the ratio of the minimum to the maximum occurring during one period of a cycle. If the mean value is zero (ie the cycle is centered on zero), then the minimum is equal and opposite in sign to the maximum. In this case, we say that R=-1. The cycle can be defined by various parameters. If we define R in terms of the stress or the strain, then R may take either positive or negative values. We might hear, for example, that R=-1 uniaxial loading is a symmetric tension / compression cycle.

Be careful about definitions, however! The Endurica material models define R in terms of the tearing energy (ie T = – dU/dA, where T is the tearing energy, U is the elastic potential energy and A is the crack area). The tearing energy is the driving force responsible for crack growth. It is always greater than or equal to zero. When R is defined in terms of tearing energy, its range is 0 ≤ R ≤ 1.

This leads to the following question that we often hear: how can Endurica compute fatigue in compression if it does not admit a negative R ratio?

Let’s look at a series of signals, all having the same strain amplitude, and each with a different mean strain. We will set the mean strain so that it is at most equal to the amplitude (corresponding to fully relaxing R=0 tension), and at least equal to the negative of the amplitude (corresponding to fully relaxing R=0 compression). In the middle of the range, we have fully reversed tension/compression (what some call “R=-1” loading when defining R in terms of strain). The principal engineering strains are plotted below for each case. This gives a smooth progression from a cycle that is only compression to a mixed cycle with both tension and compression and finally to a cycle that is only tension.

Series of signals with same strain amplitude but different Tension/Compression levels

Even for these simple uniaxial cases, the critical plane for simple compression is not the same as the critical plane for simple tension. In simple compression, due to crack closure, the critical plane is the plane that maximizes shearing. These planes make a 45-degree angle with the axis of loading (x direction). In simple tension, however, the critical plane is perpendicular to the load (x direction). In the figure below, the change in the critical plane as the mean strain increases from compression to tension is evident. On each sphere, the arrows indicate the perpendicular of a critical plane.

Mean strain increase as compression to tension is evident with change in the critical plane

The next figure shows the cracking energy density (units of mJ/mm³, and proportional to tearing energy) as a function of time on the critical plane for each case. The symbols on each line indicate the times at which the identified crack plane is open or closed. Now we can see clearly that fully reversed tension/compression (ie “R=-1” loading in terms of strain) is really R=0 when viewed in terms of tearing energy on the critical plane.

Graphs showing the cracking energy density as a function of time on the critical plane. Fully reversed tension/compression is really R=0 when viewed in terms of tearing energy.

The computed fatigue life is given in the last figure for each case using this material definition:

MAT=RUBBER
ELASTICITY_TYPE=ARRUDABOYCE
SHEAR_MODULUS=1 ! MPa
LIMIT_STRETCH=4
BULK_MODULUS=3000 ! MPa
FATIGUE_TYPE=THOMAS
FLAWSIZE=0.025 ! mm
FLAWCRIT=1 ! mm
TCRITICAL=10 ! kJ/m^2
RC=3.42E-2 ! mm/cyc
F0=2
X(R)=LINDLEY73

The computed fatigue life depending on different percentages of tension/compression

The moral of the story:

Fully reversed tension/compression cycles (“R=-1” in stress or strain terms) are really fully relaxing cycles (R=0 in tearing energy terms) from the perspective of the crack precursor on the critical plane.
The critical plane depends on whether you have tension or compression. Wohler curve analysis completely misses the fact that the failure plane is not always perpendicular to the loading direction!
A simple sinusoidal history that crosses through zero results in separate tension and compression events, each of which has its own peak and valley, and each of which influences the critical plane selection. Wohler curve analysis based on max principal stress or strain amplitude completely misses these physics.

My SAE WCX 2022 Top Takeaway

June 9, 2022April 20, 2022 by William V. Mars, Ph.D., P.E.

SAE WCX | Detroit, Michigan | April 5-7, 2022

There were several papers on fatigue life prediction for elastomers at SAE WCX 2022, but the highlight for us was this one from Automotive OEM Stellantis: “Fatigue Life Prediction and Correlation for Powertrain Torque Strut Mount Elastomeric Bushing Application” by Dr. Touhid Zarrin-Ghalami, Durability Technical Specialist at FCA US LLC with coauthors C Elango, Sathish Kumar Pandi, and Roshan N. Mahadule from FCA Engineering India Pvt, Ltd. Check out the abstract or buy the paper here…

The study shows that very accurate fatigue life prediction results are possible for elastomeric components under block cycle loading using Critical Plane Analysis. A key feature of the analysis is the characterization and modeling of rubber’s hyperelastic properties, fatigue crack growth properties, crack precursor size, and strain crystallization behavior. Careful measurement of these analysis ingredients led to a nearly perfect correlation of the predicted life (520 blocks) with the tested life (523 blocks, average of 4 replicate tests), and of predicted failure mode with observed failure mode.

Endurica users like Stellantis are developing a solid track record of routine and successful fatigue life prediction. We soon expect to see the day when CAE fatigue life prediction for rubber components is regarded as obligatory, given the risk and cost avoided with “right the first time” engineering.

Congratulations to the Stellantis team on this impressive success!

Fatigue Life (block) demonstrating the accuracy of the CAE Virtual Simulation compared to a physical test

Citation: Elango, C., Pandi, S.K., Mahadule, R.N., and Zarrin-Ghalami, T., “Fatigue Life Prediction and Correlation of Engine Mount Elastomeric Bushing using A Crack Growth Approach,” SAE Technical Paper 2022-01-0760, 2022, doi:10.4271/2022-01-0760.

Things that went right in 2020 at Endurica

June 9, 2022January 8, 2021 by William V. Mars, Ph.D., P.E.

2020 is burned in all our minds as a chaotic and tough year. Just like the rest of the world, Endurica staff experienced times of isolation and loss due to the pandemic. On a positive note, we invested heavily in making our tools and workflows better than ever so that we’re ready to come back strong in 2021. Here is a list of our top new developments in 2020:

Endurica Software Enhancements

Endurica DT’s new Ageing Feature now enables you to simulate how ageing affects your rubber product. Your compound’s stiffness, strength, and fatigue properties can all evolve with time.
Our new Linux distribution takes our solutions beyond the Windows world.
We’ve added an encryption feature to safeguard your trade secrets.
Viewer Improvements make it easier than ever to visualize your fatigue simulation results.
EIE Enhancements give you blazing-fast compute speed for full road-load signals.
We’ve also planned an aggressive development agenda for 2021. Stay tuned for a new Endurica-based smartphone app for materials engineers, for a new feature that computes fatigue threshold safety margins, for a new block cycle schedule extraction algorithm, and more!

Training

The new Fatigue Ninja Friday webinar series provides step-by-step application training for key the workflows that you need to get durability right. All of the recorded episodes are now available in the online Endurica academy.
The new Winning on Durability webinar series provides high-level overviews of both technical and business topics so you can connect Endurica tools to your strategic imperatives. All of these recorded webinars are available gratis on our website.
We’ve recast our in-person training events as LIVE, ONLINE workshops accessible safely around the world.

Testing Instruments

Coesfeld Tear and Fatigue Analyser – we hosted Coesfeld President Christian Kipscholl for one of the Winning On Durability episodes (#7). We walked through a demo of the T&FA’s fully automated, high-reliability testing workflow.
Intrinsic Strength Analyser – we hosted another Winning On Durability episode (#3) focused on understanding how a rapid cutting experiment tells us about long term fatigue behavior. We also completed a successful validation this year comparing direct measurement of the fatigue threshold with a measurement from the cutting method.

Fatigue Property Mapping Testing Service

We added the Reliability Module to our Fatigue Property Mapping testing service. Use it to quantify crack precursor size statistics when you need to estimate probability of failure.
We also reorganized the Thermal Module and the Ageing Module into Basic and Advanced levels, to offer a lower price-point when a basic option will suffice.

Want to leverage any of these new capabilities in your next durability project? Give us a call and let’s talk!

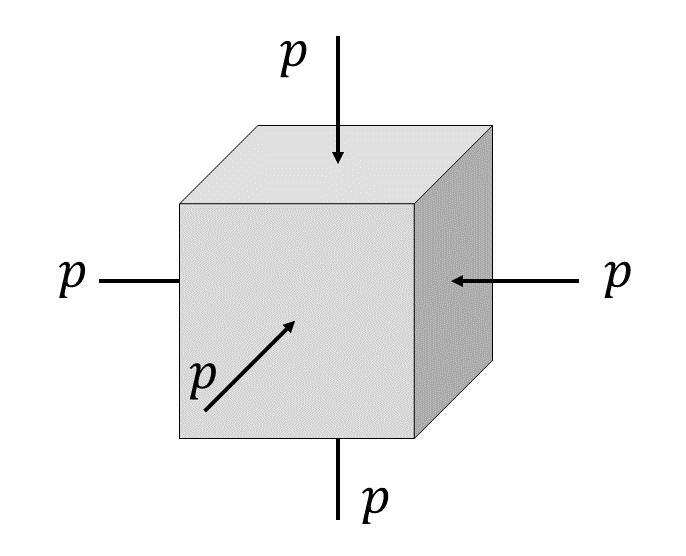
Does hydrostatic loading cause fatigue damage in rubber?

June 9, 2022January 7, 2021 by William V. Mars, Ph.D., P.E.

A question was recently put to us regarding the effects of cyclic hydrostatic loading on rubber. In hydrostatic loading, no shearing stresses are present, and the 3 principal stresses all have the same value p. For this case, all 3 Mohr’s circles degenerate to a single point on the normal stress axis.

Figure 1. Mohr’s circles degenerate to single point for the case of compressive hydrostatic pressure.

Under dynamic hydrostatic loading, the point may move along the normal stress axis in either of the tensile (p>0) or compressive directions (p<0). When we have pure hydrostatic compression, cracks in all orientations are closed with a tearing energy of zero. We expect infinite fatigue life in this case. On the other hand, when we have hydrostatic tension, growth of a crack will release energy, and so the tearing energy is positive. We then expect crack growth to occur at a rate determined by the tearing energy. Endurica estimates tearing energy T via the following rule:

in which a is the size of the crack, and W_c is the cracking energy density. For a slightly compressible material under hydrostatic loading, the cracking energy density calculation becomes

and, remembering that for volumetric deformation, the linear strain is 1/3 of the volumetric dilatation, we finally obtain

where W is the dilatational strain energy density.

So let’s compute an example using the following material definition:

Let’s compute 8 different fully relaxing hydrostatic loading cases: 4 in hydrostatic compression, 4 in hydrostatic tension. We’ll take these loaded extreme strain levels: -10%, -5%, -2%, -1%, 1%, 2%, 5%, 10%, which correspond to extreme dilatations of -27%, -14%, -6%, -3%, 3%, 6%, 16%, 33%.

As a first check, we plot the hydrostatic pressures computed for each case. The slope of the line is 3000 MPa, which agrees with the assigned bulk modulus.

Figure 2. Computed volume strain – hydrostatic pressure relationship.

Next, we compute the strain energy density and the cracking energy density for each case. As expected, we verify that for p<0, crack closure results in CED=0, and for p>0, CED=SED/3.

Figure 3. Comparison of strain energy density and cracking energy density for hydrostatic compression and tension.

Finally, we compute the fatigue life for each case. In all cases, we see that the damage sphere is uniform over its entire surface, indicating that all possible crack orientations receive equal damage. We also see that for cases involving hydrostatic compression, life is essentially infinite. For cases involving hydrostatic tension, we verify that finite life is predicted, with shorter life at higher hydrostatic tension, as expected.

Figure 4. Predicted life and damage sphere for compressive and tensile hydrostatic loading.

In summary, we have verified that the Endurica fatigue solver behaves as follows with respect to hydrostatic loading:

In hydrostatic compression, no damage accrues, and life is indefinite.
In hydrostatic tension, crack growth is predicted, with shorter fatigue life for higher values of tension. The cracking energy density is 1/3 of the strain energy density for hydrostatic tension.
For all hydrostatic cases, there is no single preferred critical plane. Rather, all planes show equal potential for crack development.

Is It Validated?

June 9, 2022January 5, 2021 by William V. Mars, Ph.D., P.E.

“Is it validated?” – that’s often the first question we hear after introducing our durability simulation capabilities. And for good reason, given the weight that hangs on the hinge of product durability. Endurica takes verification and validation (V&V) very seriously. Let’s look at what that means.

First, it means that our tools are built on well-known, well-established foundations. These foundations include 1) definition of material / crack behavior via fracture mechanics (Rivlin and Thomas, 1953), 2) integration of the crack growth rate law to predict fatigue life (Gent, Lindley and Thomas, 1964), 3) the fact that crack precursors occur naturally in all locations and all orientations in a rubber sample (Choi and Roland 1996, Huneau et al 2016), 4) hyperelastic stress-strain laws compatible with commercial FEA codes (see Muhr 2005 for an excellent review), and 5) rubber’s fatigue threshold (Lake and Thomas 1967). The validation case thus begins with the cumulative authority of thousands of reports that have confirmed these classical results over nearly 70 years.

Critical plane analysis for rubber has now been around for 20+ years, and it has been validated in multiple ways (material level, component level, system level), across multiple experimental programs (industrial and academic), by multiple independent research groups working on multiple applications (see Google/scholar, for example). It has been validated that: 1) it correctly predicts crack plane orientation under uniaxial, proportional and nonproportional loadings (Harbour et al 2008), 2) it correctly predicts fatigue life across different modes of deformation (Mars 2002), 3) it correctly accounts for the effects of crack closure (Mars 2002), 4) it correctly predicts the development of off-axis cracks for nonrelaxing cycles in strain-crystallizing materials (Ramachandran 2017), 5) it correctly predicts the effects of finite straining on crack orientation (Mars and Fatemi 2006).

The literature is full of old experiments that we have used as validation targets. We have validated Endurica’s strain crystallization models by simulating experimental results published by Cadwell et al (1940) and by Fielding et al (1943). We have validated the ability to predict deformation mode effects by simulating experimental results for simple and biaxial tension published by Roberts and Benzies (1977). We have validated Endurica’s temperature dependence against measurements reported by Lake and Lindley (1964). We have validated against multiaxial fatigue experiments reported by Saintier, Cailletaud and Piques (2006).

We’ve done our own validation experiments. My PhD dissertation (University of Toledo, 2001) contains an extensive database of tension/torsion/compression fatigue tests against which our critical plane algorithms were validated. Two additional PhD dissertations that I co-advised generated additional validations. Dr. Malik Ait Bachir’s thesis (2010) validated mathematically that the scaling law we use for small cracks is valid across all multiaxial loading states. Dr. Ryan Harbour’s thesis (2006) contains a database of multiaxial, variable amplitude fatigue experiments against which our rainflow and damage accumulation procedures were extensively validated.

Validation from partners. We partner with several testing labs. We have invested in testing protocols that produce clean, accurate data and we have run validation programs with our partners to verify the effectiveness of our testing protocols. We’ve demonstrated significant improvements to test efficiency and reproducibility (Goosens and Mars 2018) and (Mars and Isasi 2019). We’ve validated techniques for estimating precursor size and size distribution (Robertson et al 2020, Li et al 2015).

Validation from users. Three (3) of the top 12 tire companies and six (6) of the top 10 global non-tire rubber companies now use our solutions. Most of our users have run internal validation programs to show the effectiveness of our solutions for their applications. Most of these studies are unpublished, but the fact that our user base has continued growing at ~20%/year for 12 years (as of this year) says something important both about the technical validation case and the business validation case. Validation studies have been published with the US Army (Mars, Castanier, Ostberg 2017), GM (Barbash and Mars 2016), Tenneco (Goossens et al 2017) and Caterpillar (Ramachandran et al 2017).

Validation from external groups. There are several academic groups that have independently applied and validated components of our approach. There are too many to list completely, but a few recent examples include Zarrin-Ghalami et al (2020), Belkhira et al (2020) and Tobajas et al (2020).

Software verification, benchmarking and unit testing. In addition to the experimental validations mentioned above, each time we build a new version of our software, we execute a series of automated tests. These tests verify every line of code against expected function, and they ensure that as we add new features, we do not introduce unintended changes. The benchmarks include tests that verify things like coordinate frame objectivity (rigid rotations under static load should do no damage and the same strain history written in two different coordinate systems should have the same life), and check known results pertaining to material models and cycle counting rules. You can read more about our software quality processes here.

It is safe to say that no other solution for fatigue life prediction of rubber has been tested and validated against a larger number of applications than Endurica’s.

References

Aıt-Bachir, M. “Prediction of crack initiation in elastomers in the framework of Configurational Mechanics.” PhD diss., Ph. D. thesis, Ecole Centrale de Nantes, Nantes (France), 2010.

Barbash, Kevin P., and William V. Mars. Critical plane analysis of rubber bushing durability under road loads. No. 2016-01-0393. SAE Technical Paper, 2016.

Belkhiria, Salma, Adel Hamdi, and Raouf Fathallah. “Cracking energy density for rubber materials: Computation and implementation in multiaxial fatigue design.” Polymer Engineering & Science (2020).

Cadwell, S. M., R. A. Merrill, C. M. Sloman, and F. L. Yost. “Dynamic fatigue life of rubber.” Rubber Chemistry and Technology 13, no. 2 (1940): 304-315.

Choi, I. S., and C. M. Roland. “Intrinsic defects and the failure properties of cis-1, 4-polyisoprenes.” Rubber chemistry and technology 69, no. 4 (1996): 591-599.

Fielding, J. H. “Flex life and crystallization of synthetic rubber.” Industrial & Engineering Chemistry 35, no. 12 (1943): 1259-1261.

Goossens, J.R., Mars, W., Smith, G., Heil, P., Braddock, S. and Pilarski, J., 2017. Durability Analysis of 3-Axis Input to Elastomeric Front Lower Control Arm Vertical Ride Bushing (No. 2017-01-1857). SAE Technical Paper. https://doi.org/10.4271/2017-01-1857

Goossens, Joshua R., and William V. Mars. “Finitely Scoped, High Reliability Fatigue Crack Growth Measurements.” Rubber Chemistry and Technology 91, no. 4 (2018): 644-650. https://doi.org/10.5254/rct.18.81532

Harbour, Ryan Joseph. Multiaxial deformation and fatigue of rubber under variable amplitude loading. Vol. 67, no. 12. 2006.

Harbour, Ryan J., Ali Fatemi, and Will V. Mars. “Fatigue crack orientation in NR and SBR under variable amplitude and multiaxial loading conditions.” Journal of materials science 43, no. 6 (2008): 1783-1794.

Huneau, Bertrand, Isaure Masquelier, Yann Marco, Vincent Le Saux, Simon Noizet, Clémentine Schiel, and Pierre Charrier. “Fatigue crack initiation in a carbon black–filled natural rubber.” Rubber Chemistry and Technology 89, no. 1 (2016): 126-141.

Lake, G. J., and P. B. Lindley. “Cut growth and fatigue of rubbers. II. Experiments on a noncrystallizing rubber.” Journal of Applied Polymer Science 8, no. 2 (1964): 707-721.

Li, Fanzhu, Jinpeng Liu, W. V. Mars, Tung W. Chan, Yonglai Lu, Haibo Yang, and Liqun Zhang. “Crack precursor size for natural rubber inferred from relaxing and non-relaxing fatigue experiments.” International Journal of Fatigue 80 (2015): 50-57.

Mars, William Vernon. Multiaxial fatigue of rubber. 2001.

Mars, Will V. “Cracking energy density as a predictor of fatigue life under multiaxial conditions.” Rubber chemistry and technology 75, no. 1 (2002): 1-17.

Mars, W. V., and A. Fatemi. “Analysis of fatigue life under complex loading: Revisiting Cadwell, Merrill, Sloman, and Yost.” Rubber chemistry and technology 79, no. 4 (2006): 589-601.

Mars, W. V., and A. Fatemi. “Nucleation and growth of small fatigue cracks in filled natural rubber under multiaxial loading.” Journal of materials science 41, no. 22 (2006): 7324-7332.

Mars, W. V. “Computed dependence of rubber’s fatigue behavior on strain crystallization.” Rubber Chemistry and Technology 82, no. 1 (2009): 51-61. https://doi.org/10.5254/1.3557006

Mars, William V., Matthew Castanier, David Ostberg, and William Bradford. “Digital Twin for Tank Track Elastomers: Predicting Self-Heating and Durability.” In Proceedings of the 2017 Ground Vehicle Systems Engineering and Technology Symposium (GVSETS). 2017.pdf here

Mars, W. V., and M. Isasi. “Finitely scoped procedure for generating fully relaxing strain-life curves.” In Constitutive Models for Rubber XI: Proceedings of the 11th European Conference on Constitutive Models for Rubber (ECCMR 2019), June 25-27, 2019, Nantes, France, p. 435. CRC Press, 2019.

Muhr, A. H. “Modeling the stress-strain behavior of rubber.” Rubber chemistry and technology 78, no. 3 (2005): 391-425.Lake and Thomas 1967

Ramachandran, Anantharaman, Ross P. Wietharn, Sunil I. Mathew, W. V. Mars, and M. A. Bauman. “Critical Plane Selection Under Nonrelaxing Simple Tension with Strain Crystallization.” In Fall 192nd Technical Meeting of the Rubber Division, pp. 10-12. 2017.

Rivlin, R. S., and A. G. Thomas. “Rupture of rubber. I. Characteristic energy for tearing.” Journal of polymer science 10, no. 3 (1953): 291-318.Gent, Lindley and Thomas, 1964

Roberts, B. J., and J. B. Benzies. “The relationship between uniaxial and equibiaxial fatigue in gum and carbon black filled vulcanizates.” Proceedings of rubbercon 77, no. 2 (1977): 1-13.

Robertson, Christopher G., Lewis B. Tunnicliffe, Lawrence Maciag, Mark A. Bauman, Kurt Miller, Charles R. Herd, and William V. Mars. “Characterizing Distributions of Tensile Strength and Crack Precursor Size to Evaluate Filler Dispersion Effects and Reliability of Rubber.” Polymers 12, no. 1 (2020): 203. Pdf here

Saintier, Nicolas, Georges Cailletaud, and Roland Piques. “Multiaxial fatigue life prediction for a natural rubber.” International Journal of Fatigue 28, no. 5-6 (2006): 530-539.

Tobajas, Rafael, Daniel Elduque, Elena Ibarz, Carlos Javierre, and Luis Gracia. “A New Multiparameter Model for Multiaxial Fatigue Life Prediction of Rubber Materials.” Polymers 12, no. 5 (2020): 1194.

Zarrin-Ghalami, Touhid, Sandip Datta, Robert Bodombo Keinti, and Ravish Chandrashekar. Elastomeric Component Fatigue Analysis: Rubber Fatigue Prediction and Correlation Comparing Crack Initiation and Crack Growth Methodologies. No. 2020-01-0193. SAE Technical Paper, 2020.

Two Decades of Critical Plane Analysis

June 2, 2022April 1, 2020 by William V. Mars, Ph.D., P.E.

It has been 20 years since Critical Plane Analysis for rubber was first conceived and validated. There were early signs of its significance. It won awards wherever I presented it. At the 1999 SAE Fatigue Design and Evaluation meeting, it won the Henry Fuchs award. At the 2000 Tire Society meeting, it won the Superior Paper award. At the Fall 2000 ACS Rubber Division meeting, it won the Best Paper award. Upon completing my 2001 doctoral thesis, we applied for and received a US patent (2003) on it.

The strongest early sign was that I soon found myself in company with others pursuing similar thinking. The earliest was Dr. Nicolas Saintier. As far as I know, neither of us was aware of the other’s work until 2006. That was when he published an account similar enough to my own that when it came across my desk and I first started to read it, I felt certain he would cite my 2001 work as a source. I have to admit to initially feeling let down when I reached the end of his paper and found no mention of my work. I immediately looked for his other papers and found his 2001 doctoral thesis titled “Fatigue multiaxiale dans un élastomère de type NR chargé: mécanismes d’endommagement et critère local d’amorçage de fissure.” (Multiaxial fatigue life of a natural rubber: crack initiation mechanisms and local fatigue life criterion). There it was – the same founding principle of Critical Plane Analysis that I had worked so hard to articulate and validate – the idea that cracks develop on a material plane, specifically the most critical material plane, and that their localized experience drives their evolution. That we both articulated this beautifully simple and powerful principle in the same year with complete independence from each other, when no one else working on elastomers had yet spoken of this approach (there were precedents in the field of metal fatigue analysis), just shows that it was an idea whose time had come.

Although the foundational principle of Critical Plane Analysis was the same, there were also important differences between our accounts. We differed on 1) how the critical plane is selected, 2) what criterion is used to quantify the severity of loading experience by the critical plane, 3) how damage on the critical plane evolves under solicitation. The following table summarizes the key differences:

Table 1. Comparison of the Mars and Saintier Frameworks for Critical Plane Analysis.

	Mars 2001	Saintier 2001
Critical Plane Selection Method	Minimize the computed life after evaluation of damage on all planes	Maximize the principal stress prior to evaluation of damage
Multiaxial Criterion	Energy release rate estimated via cracking energy density on every plane	Stress traction on the assumed critical plane
Damage Evolution Law	Integration of crack growth rate law	Power law Wohler curve
Strain Crystallization Law	Treated as R ratio dependence of the crack growth rate law	Treated as a modifier of the stress experienced on the critical plane

It may be said that Saintier’s approach followed more closely the precedents for Critical Plane Analysis in metal fatigue, particularly with respect to the method used to select the critical plane. Selecting the plane is the first step in his method (identify the plane in order to compute the damage), but it is the last step in our method (compute the damage on each plane first and lastly pick the plane with the most damage). Saintier’s approach also depends on a Wohler curve style characterization of fatigue behavior, where ours is defined via a crack growth rate law. We have previously discussed the pros and cons of Wohler curves vs. fracture mechanics. In our approach, we placed a high priority on taking advantage of the very large pre-existing body of knowledge on the fracture mechanical behavior of elastomers, and on the economic and operational advantages that crack growth experiments enjoy.

Since my and Saintier’s first steps, there have now been many others who have contributed in various forms to the overall method, its validation and/or its application. It is safe to say that Critical Plane Analysis is here to stay, and set to continue expanding for many years (there are now several hundred research papers!).

For our part, Endurica is now in year 12 of delivering commercial grade fatigue analysis solutions built on this method. Today, Critical Plane Analysis is a production analysis workflow used by many engineering organizations to solve critical durability issues. It is the heart of the Endurica fatigue solver, and there are hundreds of trained users (look up the #fatigueninjas on twitter!). It is unrivaled for its reliability, speed and accuracy in computing the impacts of multiaxial loading on durability.

What do the next 20 years hold? We are going to see a transition in how fatigue analysis is used. OEM organizations that manage durability and risk across rubber component supply chains will transition away from receiving fatigue simulation results on an optional basis towards requiring fatigue simulations by default on every part at the inception of new programs. Expectations and achievement of cost-reduction, light weighting and sustainability initiatives will increase as product optimization begins to fully account for actual product use cases. Critical Plane Analysis has already laid the foundation for these things to happen. Older fatigue analysis methods that do not compete well against critical plane methods will become obsolete. On the research side, there will be further development of material models for use in the critical plane framework. Ageing, inelasticity, rate and anisotropy effects still need further development, for example. In 20 years, durability will be just one more thing that engineers do well every day, whether or not they know that Critical Plane Analysis was how they did it.

Mars, W. V, Multiaxial fatigue of rubber. Ph.D. Dissertation, University of Toledo, 2001.

Mars, W. V. “Multiaxial fatigue crack initiation in rubber.” Tire Science and Technology 29, no. 3: 171-185, 2001.

Mars, W. V. “Cracking energy density as a predictor of fatigue life under multiaxial conditions.” Rubber chemistry and technology 75, no. 1: 1-17, 2002.

Mars, W. V., “Method and article of manufacture for estimating material failure due to crack formation and growth.” U.S. Patent No. 6,634,236. 21 Oct. 2003.

Saintier, N, “Fatigue multiaxiale dans un élastomère de type NR chargé: mécanismes d’endommagement et critère local d’amorçage de fissure.” Ph. D Dissertation., Ecole des Mines de Paris, 2001.

Saintier, N, G. Cailletaud, R. Piques. “Crack initiation and propagation under multiaxial fatigue in a natural rubber.” International Journal of Fatigue 28, no. 1: 61-72, (2006).

Conservatism and Tradition in Fatigue Analysis

June 9, 2022January 19, 2020 by William V. Mars, Ph.D., P.E.

Slide Rule

Because Endurica’s Critical Plane Analysis is a relatively new approach to fatigue analysis of elastomers (introduced in 2001), new users often ask whether its predictions are conservative: i.e., does its predictions reliably lean in favor of safety? And is it more or less conservative than the traditional approaches it supplants?

Fatigue analysis for elastomers follows two distinct traditions. The earliest tradition traces to Sidney Cadwell’s work in 1940 which followed the even earlier ideas of metal fatigue pioneer August Wohler. This tradition is based on matching up empirical crack nucleation curves to corresponding in-service operating conditions via convenient parameters such as stress or strain. It is typically the first approach that engineers encounter in their undergraduate training, as it is often effective and relatively simple to apply. A later tradition, Fracture Mechanics, traces to the post-WWII work of Ronald Rivlin and Alan Thomas in 1953 which extended Griffith’s seminal 1921 work on rupture to elastomers. In this tradition, the energy requirements for growing a given crack provide the core organizing principle for analysis. Combined with empirical crack growth rate curves, this approach can make high accuracy life predictions for a very broad range of application scenarios. This approach is typically first encountered in graduate-level engineering programs, and due to somewhat more complicated mathematics, usually requires specialized calculation software to apply it.

There are a few big holes in the Wohler curve approach. For elastomers, perhaps the biggest limitation is that this approach assumes a priori that damage is associated with the maximum principal stress or strain. This is sometimes true for simple cases, but not always: 1) strain crystallization is known to produce off-axis cracking not aligned with the principal stress, 2) compression is known to produce cracks on planes of maximum shearing, and 3) out-of-phase multiaxial loading cases do not even possess a unique, well-defined principal direction – the directions vary in time. It is also well known that Wohler curves for rubber depend strongly on mode of deformation. Fatigue experiments in simple tension, biaxial tension, simple shear, and simple compression do not simply resolve to a single universal curve, as the Wohler approach takes for granted. To use this approach conservatively then requires that the most damaging mode of deformation – simple tension – be used as the baseline.

Perhaps the biggest limitation of the traditional Fracture Mechanics approach is that it typically focuses on only one crack at a time. In fatigue, structures begin with many microscopic cracks distributed randomly throughout. Most of the fatigue life of the structure is spent growing many small cracks. Only towards the very end of life do one or a few large cracks finally emerge as worst cases. True conservatism would mean tracking the growth of all of possible large cracks, and finding out which one(s) grow the fastest. But traditional fracture mechanics tools are not well adapted for this task. They require up front assumptions about the location and shape of the worst case crack. How can you find a worst case without considering many alternatives?

Critical Plane Analysis is simply the idea that a crack could occur anywhere in a structure, and it could occur in any orientation. It checks all of the possibilities, and it finds the worst ones. It looks at the specific loading experiences of each individual crack plane that might occur. It takes account of material behavior like strain crystallization. It takes account of crack closure conditions. It takes account of the fracture mechanical behavior of small cracks. It does not make unwarranted assumptions about the orientation of cracks. It correctly predicts the orientation of cracks for all modes of deformation. It is the most exhaustive and conservative fatigue analysis that you can do.

Don’t mistake traditional approaches with the conservative approach. Critical Plane Analysis is, by definition, the most conservative approach because it doesn’t make any assumptions about crack location or orientation, and because it checks all of the possible ways a crack might occur.

Integrated Durability Solutions for Elastomers

June 7, 2022March 16, 2018 by Christopher G. Robertson, Ph.D.

Will the durability of your new rubber product meet the expectations of your customers?

Do you have a comprehensive capability that fully integrates all of the disciplines required to efficiently achieve a targeted durability spec?

Your engineers use finite element analysis (FEA) to model the elastomer component in the complex geometry and loading cycle for the desired product application. One traditional approach to predicting durability is to develop a rough estimate of lifetime by looking at maximum principal strain or stress in relation to strain-life or stress-life fatigue curves obtained for the material using lab specimens in simple tension. The difficulties and uncertainties with this method were discussed in a recent blog post.

a rough estimate of lifetime by looking at maximum principal strain or stress in relation to strain-life or stress-life fatigue curves obtained for the material using lab specimens in simple tension

A modern approach to elastomer durability is to use the Endurica CL™ durability solver for FEA. This software uses rubber fracture mechanics principles and critical plane analysis to calculate the fatigue lifetime – which is the number of times the complex deformation cycle can be repeated before failure – for every element of the model. This provides engineers with the ability to view lifetime throughout the FEA mesh, allowing them to modify design features or make material changes as needed to resolve short-lifetime areas.

view lifetime throughout the FEA mesh, allowing them to modify design features or make material changes as needed to resolve short-lifetime areas.

A sound finite element model of the elastomer product in the specified loading situation and fundamental fatigue material parameters from our Fatigue Property Mapping™ testing methods are the two essential inputs to the Endurica CL software. This is illustrated in the figure below.

The requisite elastomer characterization methods can be conducted by us through our testing services or by you in your laboratory with our testing instruments. For some companies, consulting projects are a route to taking advantage of the software before deciding to license the unique predictive capabilities. The following diagram shows how our products and services are integrated.

Durability Solutions for Elastomers

For companies that are just getting started with implementing our durability solutions, the following is a typical testing services and consulting project:

We use our Fatigue Property Mapping™ testing methods, through our collaboration with Axel Products Physical Testing Services, to characterize the properties of cured sheets of rubber compounds sent to us by the client. The minimum requirements for fatigue modeling are crack precursor size and crack growth rate law, and these are quantified within our Core Fatigue Module. Special effects like strain-induced crystallization and aging/degradation are accounted for using other testing modules when applicable.
The client sends us the output files from their finite element analysis (FEA) of their elastomer part design for the deformation of their complex loading cycle. It is common for the goal to be a comparison of either two designs, two distinct loading profiles, two different rubber compounds, or combinations of these variations. Our software is fully compatible with Abaqus™, ANSYS™, and MSC Marc™, so the simulations can be conducted on any of these FEA platforms. In some situations where a client does not have their own FEA capabilities, one of Endurica’s engineers will set up the models and perform the analyses instead.
The fatigue parameters and FEA model are inputted to Endurica CL fatigue solver to calculate values of the fatigue lifetime for every element of the model. The lifetime results are then mapped back onto the finite element mesh in Abaqus, ANSYS, or MSC Marc so that the problem areas (short lifetime regions) within the geometry can be highlighted.
We review the results with the client and discuss any opportunities for improving the fatigue performance through design and material changes.

Advanced implementors of our durability solutions have licensed the Endurica CL software and are using our rubber characterization methods in their laboratories on a routine basis, with instruments provided through our partnership with Coesfeld GmbH & Co. (Germany). One recently publicized example of a company using the Endurica approach to a very high degree is Tenneco Inc., which you can read about here.

We want to help you #GetDurabilityRight, so please contact us at info@endurica.com if you would like to know more about how Endurica’s modern integrated durability solutions for elastomers can help enable a product development path that is faster, less expensive, and more confident.