Crystallization requires the suppression of molecular mobility, which in natural rubber can happen either by reducing the temperature or by increasing the strain. Crystallization of natural rubber can be extremely beneficial to durability. Nonrelaxing conditions (ie R>0) can increase life by factors of more than 100! So, what happens if you have both high mean strain and high temperature?
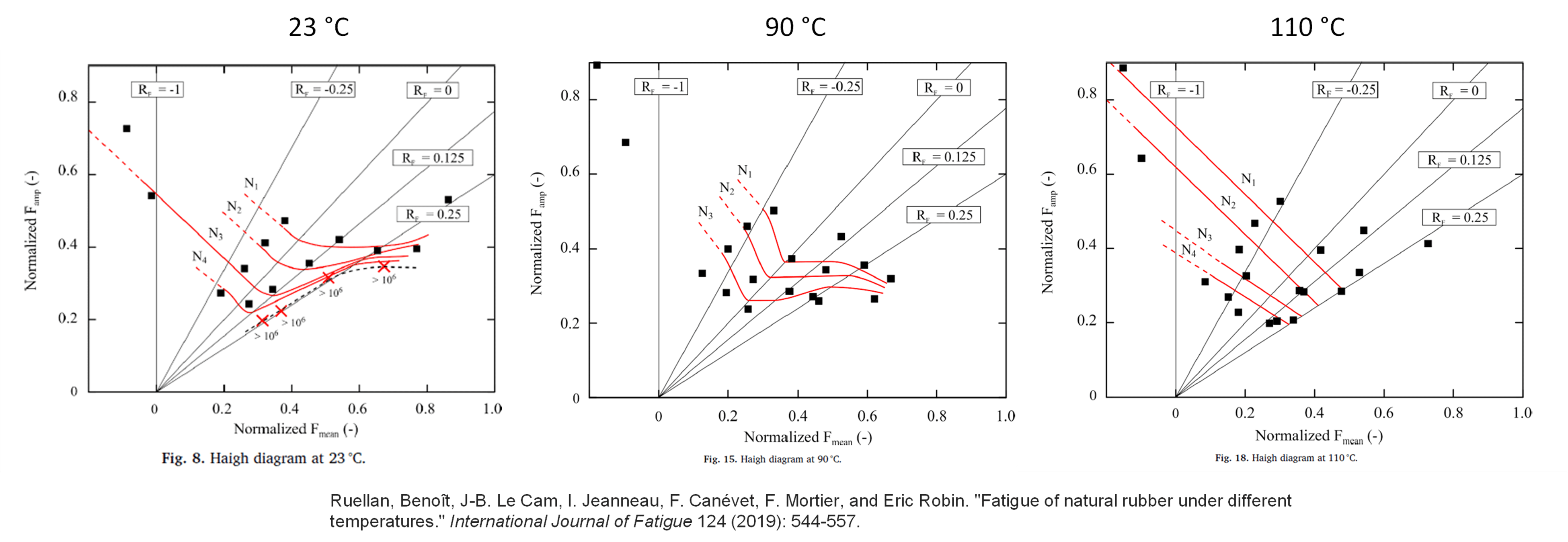
This was the question studied in 2019 by Ruellan et al. They constructed Haigh diagrams for a filled natural rubber at 3 temperatures: 23 degC, 90 degC and 110 degC. They completed a large experimental study using dumbbell shaped specimens with a matrix consisting of approximately 4 R ratios x 4 amplitudes x 3 temperatures = 48 conditions. Their results show that the increase of fatigue life with increasing mean strain at constant amplitude disappears as temperature is increased. In particular, notice how at 23 degC each life contour (shown in red) has a strongly defined minimum force amplitude that lies near the R=0 line. Also notice how, at higher temperatures, the life contours start to reflect a decrease of life with increasing mean strain.
This interesting effect can easily by replicated in the Endurica fatigue solver by letting the strain crystallization effect depend on temperature. The material definition we have used in this quick demo is given below in both the old hfi format and the new Katana json format. I have highlighted in yellow those parts of the definition which reflect the temperature dependence.

In the material definition, we have reflected two behaviors:
- the increase of crack growth rate with temperature (ie the RC parameter), and
- the decrease of strain crystallization with temperature (ie the Mars-Fatemi exponential strain crystallization parameter FEXP).
We have plotted the resulting Haigh diagrams in the Endurica viewer, and directly overlaid Ruellan’s results for comparison. Although the x and y scales in Ruellan’s results are shown in terms of total specimen force and ours are shown in terms of strain, a quite satisfying match is nonetheless achieved for the interaction of temperature with the mean strain effect. It is especially satisfying that such rich behavior is so compactly and so accurately described by means of the Mars-Fatemi crystallization parameter.