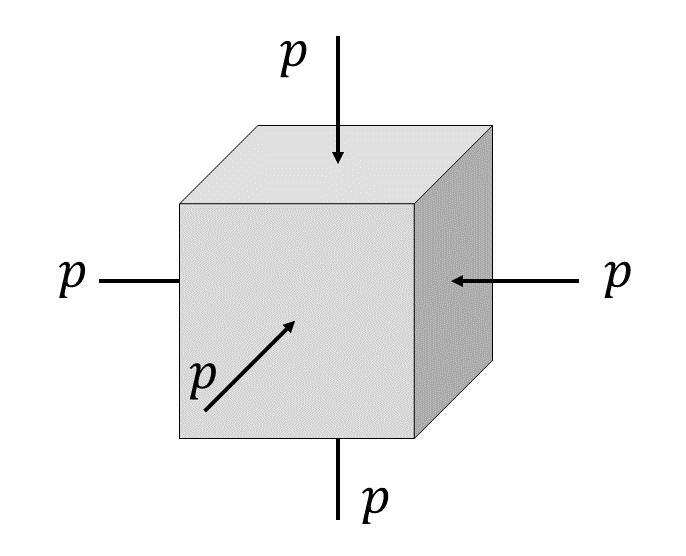
A question was recently put to us regarding the effects of cyclic hydrostatic loading on rubber. In hydrostatic loading, no shearing stresses are present, and the 3 principal stresses all have the same value p. For this case, all 3 Mohr’s circles degenerate to a single point on the normal stress axis.
Figure 1. Mohr’s circles degenerate to single point for the case of compressive hydrostatic pressure.
Under dynamic hydrostatic loading, the point may move along the normal stress axis in either of the tensile (p>0) or compressive directions (p<0). When we have pure hydrostatic compression, cracks in all orientations are closed with a tearing energy of zero. We expect infinite fatigue life in this case. On the other hand, when we have hydrostatic tension, growth of a crack will release energy, and so the tearing energy is positive. We then expect crack growth to occur at a rate determined by the tearing energy. Endurica estimates tearing energy T via the following rule:
in which a is the size of the crack, and Wc is the cracking energy density. For a slightly compressible material under hydrostatic loading, the cracking energy density calculation becomes
and, remembering that for volumetric deformation, the linear strain is 1/3 of the volumetric dilatation, we finally obtain
where W is the dilatational strain energy density.
So let’s compute an example using the following material definition:
Let’s compute 8 different fully relaxing hydrostatic loading cases: 4 in hydrostatic compression, 4 in hydrostatic tension. We’ll take these loaded extreme strain levels: -10%, -5%, -2%, -1%, 1%, 2%, 5%, 10%, which correspond to extreme dilatations of -27%, -14%, -6%, -3%, 3%, 6%, 16%, 33%.
As a first check, we plot the hydrostatic pressures computed for each case. The slope of the line is 3000 MPa, which agrees with the assigned bulk modulus.
Figure 2. Computed volume strain – hydrostatic pressure relationship.
Next, we compute the strain energy density and the cracking energy density for each case. As expected, we verify that for p<0, crack closure results in CED=0, and for p>0, CED=SED/3.
Figure 3. Comparison of strain energy density and cracking energy density for hydrostatic compression and tension.
Finally, we compute the fatigue life for each case. In all cases, we see that the damage sphere is uniform over its entire surface, indicating that all possible crack orientations receive equal damage. We also see that for cases involving hydrostatic compression, life is essentially infinite. For cases involving hydrostatic tension, we verify that finite life is predicted, with shorter life at higher hydrostatic tension, as expected.
Figure 4. Predicted life and damage sphere for compressive and tensile hydrostatic loading.
In summary, we have verified that the Endurica fatigue solver behaves as follows with respect to hydrostatic loading:
- In hydrostatic compression, no damage accrues, and life is indefinite.
- In hydrostatic tension, crack growth is predicted, with shorter fatigue life for higher values of tension. The cracking energy density is 1/3 of the strain energy density for hydrostatic tension.
- For all hydrostatic cases, there is no single preferred critical plane. Rather, all planes show equal potential for crack development.
