Some Thoughts on Crack Growth and Fracture Testing in Polymers

My PhD work at the University of Wisconsin was on crack growth in high density, high molecular weight polyethylene (HDHMWPE) used in natural gas distribution pipelines1. This semi-crystalline, thermoplastic material like many other plastics exhibits a yielding mechanism in addition to nonlinear viscoelastic effects which made the material characterization and modeling aspect of the work very challenging. For fracture, the yielding mechanism creates a significant specimen thickness effect similar to the effect found in most metals. The yielding mechanism can create 3D effects on fracture surfaces due to some areas yielding before fracture and other areas fracturing without yielding first, normally labeled as areas of plane stress and plane strain, respectively. Thicker fracture specimens have a greater proportion of the material in a state of plane strain. This effect is shown in the diagram below. In metals, it is important to measure the plane strain fracture toughness, K_IC.

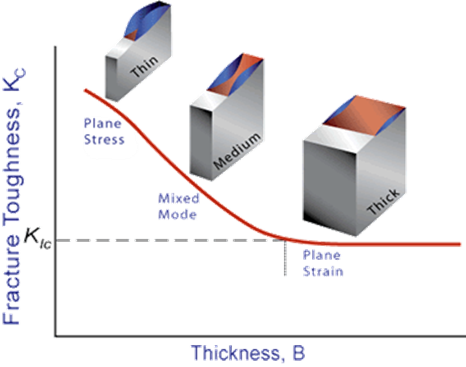
The yielding in HDHMWPE specimens creates a similar thickness effect even though the mechanism of yielding is different than that in metals. The picture here shows 4 specimens from my PhD work illustrating this thickness effect.

These are fracture surfaces from double edge cracked creep specimens. The yielding phenomena causing the stress-whitening due to the highly drawn material is notably more present on the thinner specimens. The thickness effect on the surfaces is similar to those in the previous sketch even though there are differences due to the different material and the creep loading. The 3D effects on the fracture surfaces complicate the results interpretation and application of available theories.

On a side note, I was using a technique called “Intrinsic Moiré” to measure the surface strains on the specimens while the cracks grew. A picture is shown in the next image.

The fringes are lines of constant relative displacement that can be differentiated to calculate surface strains. With the 3D fracture effects beneath the surface shown above there is obviously much more going on through the thickness that surface strains do not reveal.

As a graduate student (a few decades ago) I was giving a talk on this work at conference, and after the talk two young professors from South Carolina came up to me and asked me to attend their lecture later that day. Their names were Mike Sutton and Wally Peters. Their talk described a new method where they would splatter spray paint on the specimen surface and then track the displacement of the small paint shapes using 2 digital cameras and triangularization. This was the birth of the now widely known “Digital Image Correlation” or DIC method. OK, end of the side note.

When I started work at Goodyear, I was delighted to learn that rubber, and most elastomers, do not have a yielding mechanism and thus, they should not have a thickness effect, or a related dependance on deformation mode (tensile, in-plane, or out-of-plane shear). Some work had been done by the founding fathers of fracture mechanics in elastomers on the question of mode of deformation, and they showed that a tensile specimen and a trouser tear specimen (like an out-of-plane shear fracture mode) will give equivalent tear strengths ( T_C) but this was less than satisfying for demonstrating an independence on thickness, since they are both done with thin specimens. The extensibility of rubber causes the deformation to be predominately tension in the tearing region, irrespective of how the crack is opened, such that TC values are similar for rubber evaluated in different testing modes.2,3

At Goodyear, we decided to pursue both questions of thickness and deformation mode by looking at a torsional crack growth specimen vs. common edge-cracked tensile specimens. The geometry of the torsional specimen is shown below with a circumferential crack in a torsional disk. The disk could be put in different combinations of tension and torsion cycles. It behaves like a very thick specimen, since the dimension of interest for thickness is around the circumference. A circumferentially cut crack at the mid-height will grow inward at decreasing rates, since the energy release rate goes down as the crack grows.

I worked on this with collaborators at Goodyear and outside of Goodyear including Alan Gent, Oon-Hock Yeoh, Hamid Aboutorabi, Tom Fleischman and Vladimir Kerchman⁴ Will Mars also looked at a similar specimen as part of his PhD and other works⁵. Measuring the amount of crack growth was challenging, but we managed with a direct observation with the crack opened, and with a stiffness reduction technique. In addition to being ”thick”, this specimen also produced “Mode III”, out-of-plane shear fracture deformation.

We were able to produce some nice planar crack surfaces without 3D effects as shown in the picture below for a carbon black filled SBR .

Plotting the crack growth rates vs energy release rate measurements to those reported for edge cracked simple tension showed that the two tests produced largely the same results. This validated the claims that rubber should not have either a thickness effect or a mode-of-deformation effect. The decrease in crack growth rates for the torsional specimen at low energy release rates is due to eventual out-of-plane cracking towards the end of the test. Each test begins at high energy release rates and progresses to low energy release rates.

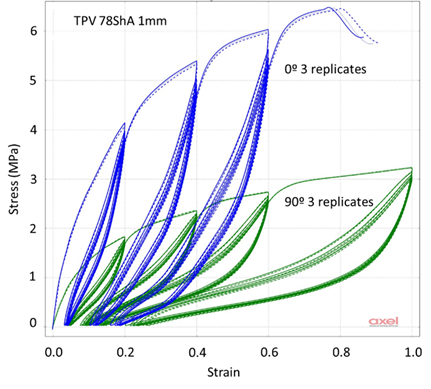
Fast-forward to today, and at Endurica, along with some partners, we are embarking on a journey to provide improved durability predictions for thermoplastic elastomers, or TPEs. A common TPE that has been around for a few decades, is Santoprene which is in a sub-category called Thermoplastic Vulcanizates or TPVs. It is a direct combination of a thermoplastic, polypropylene, and an elastomer, EPDM to create the immiscible blended TPE. And, yes, since it has the thermoplastic component, it also has a yielding mechanism and plasticity as shown in the stress-strain curves below⁶.

As shown, it has the added complication of producing anisotropic results, since the specimens are injection molded and the polypropylene phase becomes elongated in the flow direction.

Fracture surfaces for this material are also shown below, and the 3D effects on the surfaces due to the yielding mechanism are apparent.

And, so, the journey continues.

References

 1. Ebbott T G, “Fracture Characteristics of a Viscoelastic Polymer under Constant Load: Experiments and Analysis”, PhD Thesis, University of Wisconsin-Madison, 1987.

2. Lake, G.J., “Fatigue and Fracture of Elastomers”,  Rubber Chem. Technol. 1995, 68, 435-460.

3.     3.   Rivlin, R.S.; Thomas, A.G. “Rupture of rubber. I. Characteristic energy for tearing”, J. Polym. Sci. 1953, 10, 291–318.

4.    4.   Fleischman, T.S., V. Kerchman, T. G. Ebbott, “Torsional Crack Growth Test to Simulate Belt Edge Deformation”, Tire Sci. Technol. 29, 91 (2001).

5.     5.  Mars, W.V.; Fatemi, A., “A literature survey on fatigue analysis approaches for rubber”, Int. J. Fatigue 2002, 24, 949–961.

6.     6.  Burgoa, A., Zulueta, K., Mars, W.V., Ebbott, T.G., and M. Bauman, “Hyperelastic-viscoplastic and crack growth behavior of thermoplastic vulcanizates (TPVs)”, Constitutive Models for Rubber XIII, Dal (Ed), 2025.

7.     7.  Mars, W. V., & Fatemi, A. (2004). A novel specimen for investigating the mechanical behavior of elastomers under multiaxial loading conditions. Experimental mechanics, 44(2), 136-146.