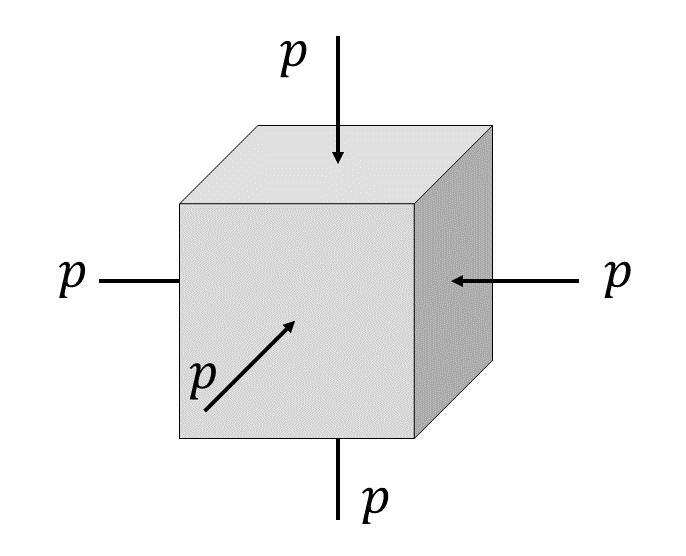
A question was recently put to us regarding the effects of cyclic hydrostatic loading on rubber. In hydrostatic loading, no shearing stresses are present, and... Continue reading
- We Offer
Elastomer Durability Analysis Solutions
Discover the Science Behind Elastomer Fatigue
Take your designs to the next level with models tailored specifically for rubber materials.
- Industry Solutions
- Resources
- About
- Contact
“Is it validated?” – that’s often the first question we hear after introducing our durability simulation capabilities. And for good reason, given the weight that... Continue reading
The old saying “loose lips sink ships” is as true in product development as it is in war. Maybe more so – while warships are... Continue reading
It has been 20 years since Critical Plane Analysis for rubber was first conceived and validated. There were early signs of its significance. It won... Continue reading
We have just launched a few updates to our Fatigue Property Mapping service offerings. The changes were: Addition of the all new Reliability Module for... Continue reading
Because Endurica’s Critical Plane Analysis is a relatively new approach to fatigue analysis of elastomers (introduced in 2001), new users often ask whether its predictions... Continue reading
“I tell my suppliers to use you all the time.” – Exact words from an engineer in charge of purchasing key components for a major... Continue reading
A brand promise of durability (i.e. fitness for service over a suitable period) doesn’t mean much unless it is delivered reliably (i.e. with high consistency). ... Continue reading
Ever thought about what it takes to deliver the durability you expect from products you use? Durability reflects the combined sum of many decisions made... Continue reading
When people ask me what Endurica does I tell them: You give us a computer file of one full use cycle of your design –... Continue reading
Showing 31–40 of 51 posts
Recent Posts
- Multi-Year Maintenance & Support Bundles for Perpetual License Holders
- Engineering Failure Analysis — published in affiliation with European Structural Integrity Society
- Taming the Tarmac: Simulating Tire Durability on the Nürburgring
- Rubber Fatigue ≠ Metal Fatigue Part 3: Thermal Effects
- 4-in-1: Community Conference
Categories
No comments to show.
© 2025 Copyright Endurica LLC
Website Designer iGo Sales and Marketing, Inc.