The load cases to be considered in fatigue analysis can be very lengthy and can involve multiple load axes. Often, load cases are much longer than can be calculated via direct time-domain finite element analysis (FEA).
In metal fatigue analysis, linear superposition is a widely used technique to generate stress-strain history from road loads [1], [2], [3]. When structures behave linearly, this approach is accurate and computationally efficient, allowing the analysis of lengthy load signals. For single axis problems, the finite element (FE) solution for a single unit load case is simply scaled according to the input load history. For multiaxial problems, unit load cases are solved for each of the axes, then scaled and combined according to the input load history.
Due to rubber’s 1) nonlinear material behaviour, 2) nonlinear kinematics, and 3) the possibility of nonlinear contact, linear superposition cannot be applied to rubber fatigue analysis. This article is the second in a series examining how rubber fatigue analysis procedures differ from those used for metal fatigue. Here we present the Endurica EIETM (Endurica Interpolation Engine) solver, which is a tool for the rapid generation of stress-strain histories for fatigue analysis in cases where linear superposition fails.
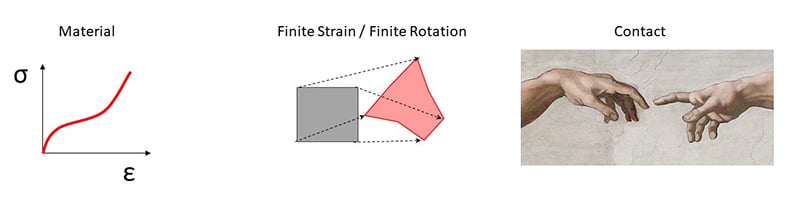
Fig.1. Nonlinearity figures in the analysis of rubbery materials in several ways including material nonlinearity, kinematic nonlinearity, and contact linearity. Endurica’s EIE solver provides an efficient and accurate method for generating stress-strain history when there is strong nonlinearity.
Brief review of the linear superposition procedure for metals
For linear structures, the relationship between forces [F] and displacements [u] can be written as a matrix multiplication where [k] is the stiffness matrix.
[F] = [k][u]
The associative property of function composition means that multiplying the displacements by a scalar a produces proportionally larger forces.
a[F] = [k](a[u])
The distributive property of addition means that a force system resulting from combined displacements [u] and [v]
[F] = [k][u] +[k][v]
can also be calculated as
[F] = [k]([u] + [v])
Similarly, stress and strain fields can be scaled and combined by linear superposition. Engineers have been using this principle for many years in metal fatigue analysis, particularly for treating multiaxial cases arising from field-recorded load-displacement histories.
The stress and strain fields in a part are assumed to result from a linear combination of unit load cases, where the scale factor for each unit load case is applied to the stress or strain field corresponding to a given input channel.
For example, for the beam shown in Fig.2, if channel 1 is the unit displacement u with magnitude a(t), and channel 2 is another unit displacement v elsewhere in the structure with magnitude β(t) , then the entire history of stress and strain at all points in the beam can be recovered by linear superposition.
Note that the FE solver only needs to produce a single time-independent solution for each unit load case. The time dependence of the solution is obtained entirely through the time variations of the scale factors a(t) and β(t). This extremely efficient method has been used for many years in metal fatigue analysis. It allows rapid analysis of complete road load histories consisting of millions of time steps.
Fig.2. Linear superposition of single load case FE solutions has long been used to generate stress-strain histories from road load histories in metal fatigue analysis.
Endurica EIETM: load space discretization and interpolation for nonlinear cases
Solving the nonlinear case requires a completely different approach. We wish to retain the advantages of efficiently constructing stress-strain time histories from precomputed FE solutions. Instead of precomputing a single unit load case for each input channel, we precompute a set of load cases from a discretized load space. We call this set a map.
The number of load cases in the map must be sufficient so that we can use interpolation to obtain an reasonable approximation of the nonlinear response at any point within the map. Fig.3 shows a map with two channels defined by x and z displacements. The blue points in the map are precalculated using an FE solver such as Ansys or LS-Dyna following the path traced by the blue line. Once the map is defined, the stress-strain history along the red line can be interpolated from the precomputed solutions in the map.

Fig.3. Two-channel map discretizing a space defined by the x and z displacements. Blue dots represent FE solutions for which the stress-strain fields are precomputed. The blue line represents a solution path, which defines the order in which the solutions are computed and stored in the results database. The red line represents a possible actual displacement history. The stress-strain history for points on the red path is obtained by interpolation from points on the precomputed map.
Endurica EIETM is a general purpose tool for creating and using non-linear maps to generate stress-strain histories for fatigue analysis [4], [5]. EIE is an abbreviation for efficient interpolation engine. EIE provides a simple workflow and powerful utilities for creating and using maps for interpolation. It supports up to six independent input channels.
The entire EIE workflow consists of three main steps. The first step is to create a map. The next step is to specify your history in terms of forces or displacements. Note that any quantity that can be applied as a boundary condition to the FE model can be set up as a channel. The last step is to perform the specified interpolation. The process produces a time history of strain tensor components for each element in your FE model.
The map creation process involves four steps, as shown in Fig.4. First, the number of independent channels that will be used to specify the history must be defined. The map type must also be specified. Several types are available, including a completely customizable map. Grid-based maps are often appropriate for one-, two- and three-dimensional maps. For higher dimensional maps, case vector-based maps are often the most convenient.
Once the map type has been defined, EIE generates solution paths. These consist of enumerated load states that should be applied as boundary conditions to the FE model to generate the map. One or more paths may be generated depending on map type. Each path is called a branch. For each branch, EIE writes a file with the appropriate boundary condition history, which is necessary for the generation of the map. Next, the FE model is set up and executed using EIE’s boundary conditions. Finally, the database of FE results is linked to the corresponding branch in the definition of the map.
At this point the map is complete and ready for interpolation. Note that linear superposition can be implemented as a special case in EIE when unit load case solutions are collected and defined as a map. In general, however, a non-linear map will contain a greater number of solution steps.

Fig.4. Steps to specify a map for use by Endurica EIETM.
Specifying the load history is as simple as selecting a file containing the time history of each input channel. In the file, each row represents one time step and each column represents an input channel. EIE supports .csv and .rsp formats, both common data formats. Fig.5 shows an example history with and displacements. Note that the range of displacements in the history should not exceed the range of the precalculated map. Although interpolated solutions can be quite accurate, extrapolation for non-linear problems can be very risky and inaccurate.

Fig.5. Example two-channel displacement history for interpolation.
Once the map and history are specified, interpolation can begin. Endurica EIETM supports multi-threading, meaning that interpolation calculations can be distributed and executed in parallel across available CPUs. This makes interpolating very fast and very scalable to large models and lengthy histories. Note that Endurica EIETM generates large files because it calculates stress and strain tensor components for each time step of each finite element. It is therefore important to ensure that you have sufficient disk space available when running Endurica EIETM.
Comparing linear and non-linear interpolation results for a sway bar under uniaxial loading
As a first example, consider an automotive sway bar link, shown in Fig.7. The sway bar transmits load in a single axial direction. This model uses Ogden’s hyper elastic law, which involves a non-linear relationship between stress and strain. The large deformation solution also involves non-linear kinematics due to the incompressibility of rubber and finite displacements and rotations. To compare the linear and non-linear interpolation methods, we will run the analysis using both: 1) the linear scaling method (where the map consists of a single load case in which we apply one newton of total load in the x-direction to the link and solve for the strain distribution in the part); and 2) the non-linear method (where the map consists of 11 precomputed steps ranging from -10000N to +10000N).

Fig.6. Sway bar link under uniaxial loading (left). Axial load history input for strain history interpolation (right).
Figs. 8–10 show the six engineering strain tensor component history results for both the linear superposition procedure (left) and the nonlinear EIE procedure (right). The results are shown for three different locations on the sway bar bushing (highlighted in red). The largest strain component is the 31 shear (orange line). Note that for the linear procedure, a linear increase in the amplitude of the global force results in a linear increase in the strain components. The non-linear procedure produces quite different results. In fact, where the linear solution predicts symmetry of tension and compression loads, the non-linear solution correctly captures asymmetries.

Fig.7. Comparison of linear (left) and non-linear (middle) interpolation results for strain tensor components at the location indicated on the right.
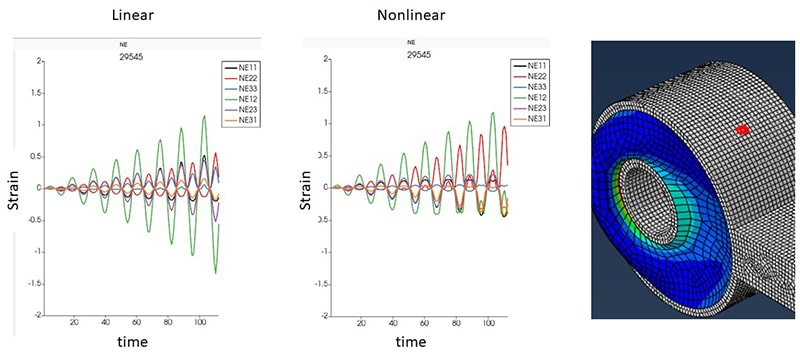
Fig.8. Comparison of linear (left) and non-linear (middle) interpolation results for strain tensor components at the location indicated on the right.

Fig.9. Comparison of linear (left) and non-linear (middle) interpolation results for strain tensor components at the location indicated on the right.
As a final comparison, Fig.11 shows the fatigue life calculated using Endurica CLTM. A longer fatigue life is predicted for the non-linearly interpolated case compared to the linearly interpolated case. Note that the fatigue damage is more concentrated in the linear case and more spatially distributed for the non-linear solution.

Fig.10. Comparison of fatigue life calculations based on linear (left) and non-linear (right) interpolated strain history.
Endurica EIETMvalidation for a six-channel non-linear interpolation
As a further test of the non-linear interpolation procedure for a six-channel ( forces + moments) multiaxial load analysis of the gearbox mount shown in Fig.11, the map shown in Fig.12 was defined. This map contained 51 precalculated non-linear FE solutions. The complete loading history to be interpolated is shown in Fig.13. This history was solved in full directly and interpolated from the map using Endurica EIETM.

Fig.11. Gearbox mount analysis. All forces and moments (x, y, and z) were applied at the centre of the top rigid mounting plate.

Fig.12. Six-channel map containing 51 precalculated finite element solutions.

Fig.13. Full six-channel road load history used for validation analysis of gearbox mount.
The strain tensor histories for the 11, 22 and 12 strain components are compared between the directly solved and interpolated solutions in Fig.14 at the location of the most critical element. A fairly accurate interpolation was obtained with a much shorter run time than the direct finite element analysis of the full history.

Fig.14. Comparison of EIE-interpolated strain components (blue) v. direct finite element solution (red) at the location of the most critical element.
The fatigue life of the gearbox mount was calculated with Endurica CLTM using both the EIE-interpolated strain history and the directly solved strain history. The fatigue contours for both cases are shown in Fig.15. The fatigue life for the interpolated history was 7.52E8 and for the directly solve history the fatigue life was 7.87E8. These results indicate a close agreement between the EIE and directly solved cases. Other validation cases were recently published elsewhere (Mars et al 2024).

Fig.15. Comparison of fatigue life calculated from EIE-interpolated strain components (right) and direct finite element solution (left).
Conclusion
Analysis of rubber components typically involves strong nonlinearities due to material behaviour, finite strain kinematics, and contact. The traditional linear superposition of unit load cases, widely used in metal fatigue analysis, is not effective in such cases. Fortunately, the Endurica EIETM solver can generate strain histories efficiently and accurately in these cases. The EIE tools allow the analysis to precalculate a set of FE solutions for efficient discretization of the load space and accurate interpolation of signals within the load space. With sufficient discretization of the load space, it was shown that quite accurate results can be produced for cases where there are between one and six load input channels.
References
[1.] R. W. Landgraf, “Applications of fatigue analyses: transportation”, Fatigue ’87, vol. 3, pp. 1593–1610, 1987
[2.] Moon, Seong-In et al, “Fatigue life evaluation of mechanical components using vibration fatigue analysis technique”, Journal of Mechanical Science and Technology, vol. 25, pp. 631–637, 2011.
[3.] F. A. Conle and C. W. Mousseau, “Using vehicle dynamics simulations and finite-element results to generate fatigue life contours for chassis components”, International Journal of Fatigue, vol. 13(3), pp. 195–205, 1991.
[4.] K. P. Barbash and W. V. Mars, “Critical plane analysis of rubber bushing durability under road loads”, SAE Technical Paper No. 2016-01-0393, 2016.
[5.] W. V. Mars, “Interpolation engine for analysis of time-varying load data signals”. U.S. Patent 9, 645, 041, May 9, 2017.
[6.] W. Mars, K. Barbash et al, “Durability of Elastomeric Bushings Computed from Track-Recorded Multi-Channel Road Load Input”, SAE Technical Paper No. 2024-01-2253, 2024.