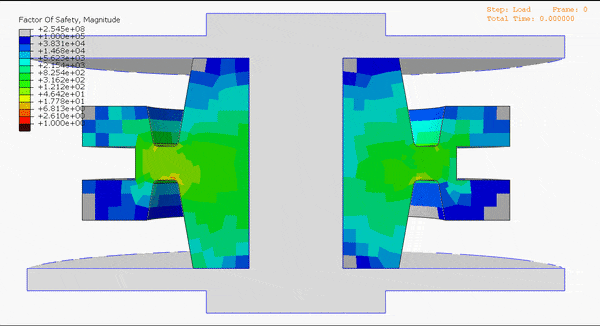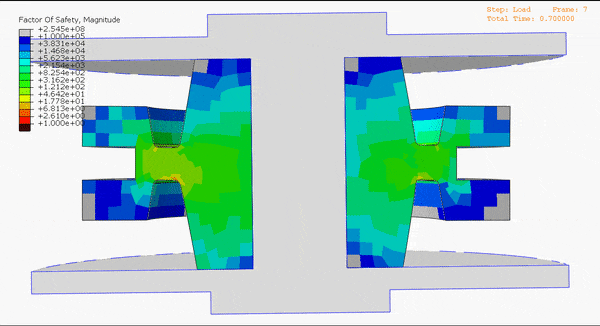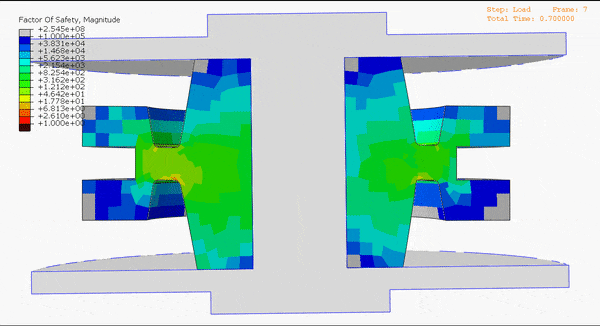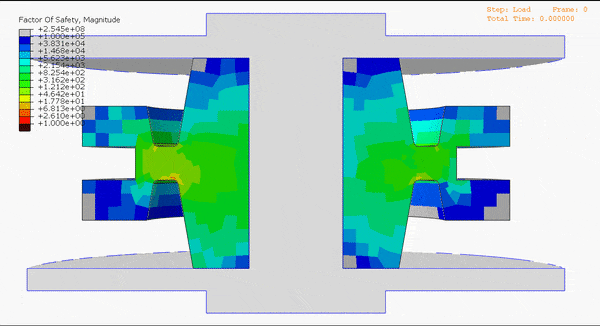
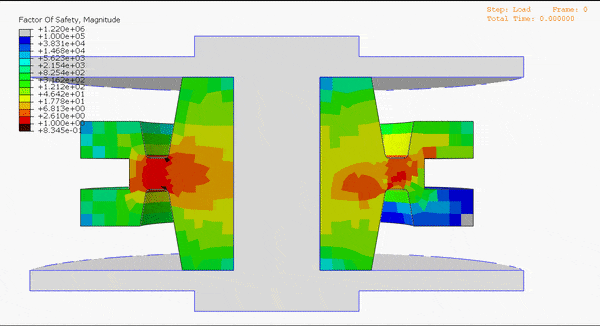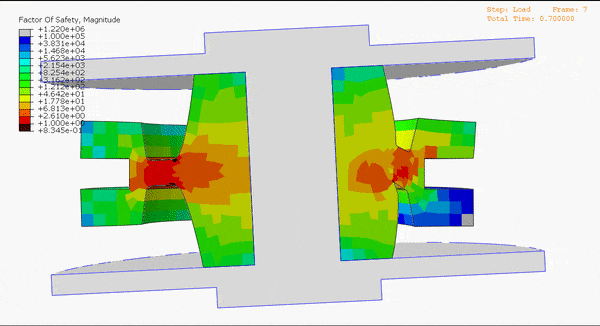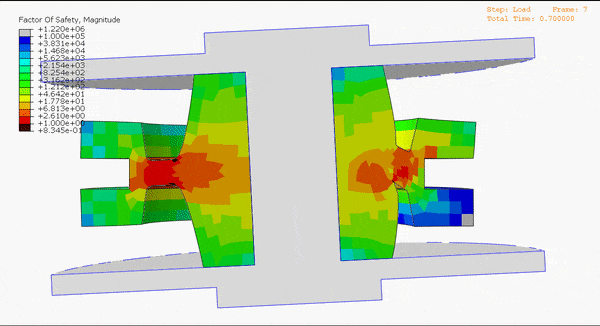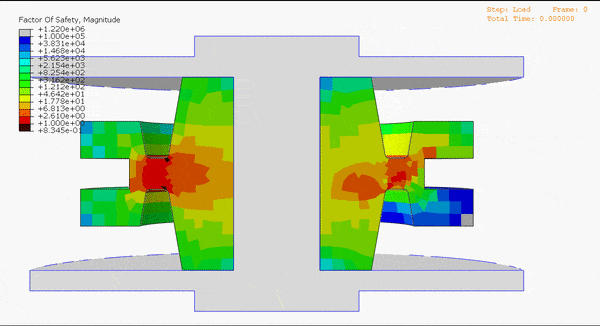
“Is it validated?” – that’s often the first question we hear after introducing our durability simulation capabilities. And for good reason, given the weight that hangs on the hinge of product durability. Endurica takes verification and validation (V&V) very seriously. Let’s look at what that means.
First, it means that our tools are built on well-known, well-established foundations. These foundations include 1) definition of material / crack behavior via fracture mechanics (Rivlin and Thomas, 1953), 2) integration of the crack growth rate law to predict fatigue life (Gent, Lindley and Thomas, 1964), 3) the fact that crack precursors occur naturally in all locations and all orientations in a rubber sample (Choi and Roland 1996, Huneau et al 2016), 4) hyperelastic stress-strain laws compatible with commercial FEA codes (see Muhr 2005 for an excellent review), and 5) rubber’s fatigue threshold (Lake and Thomas 1967). The validation case thus begins with the cumulative authority of thousands of reports that have confirmed these classical results over nearly 70 years.
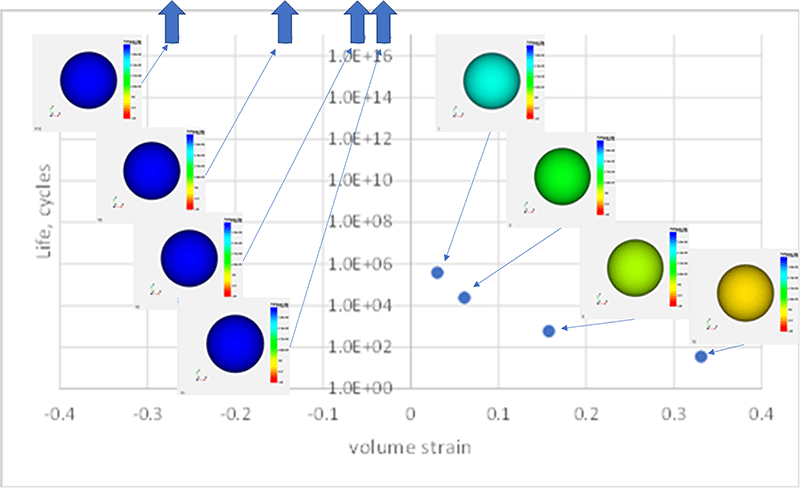
Critical plane analysis for rubber has now been around for 20+ years, and it has been validated in multiple ways (material level, component level, system level), across multiple experimental programs (industrial and academic), by multiple independent research groups working on multiple applications (see Google/scholar, for example). It has been validated that: 1) it correctly predicts crack plane orientation under uniaxial, proportional and nonproportional loadings (Harbour et al 2008), 2) it correctly predicts fatigue life across different modes of deformation (Mars 2002), 3) it correctly accounts for the effects of crack closure (Mars 2002), 4) it correctly predicts the development of off-axis cracks for nonrelaxing cycles in strain-crystallizing materials (Ramachandran 2017), 5) it correctly predicts the effects of finite straining on crack orientation (Mars and Fatemi 2006).
The literature is full of old experiments that we have used as validation targets. We have validated Endurica’s strain crystallization models by simulating experimental results published by Cadwell et al (1940) and by Fielding et al (1943). We have validated the ability to predict deformation mode effects by simulating experimental results for simple and biaxial tension published by Roberts and Benzies (1977). We have validated Endurica’s temperature dependence against measurements reported by Lake and Lindley (1964). We have validated against multiaxial fatigue experiments reported by Saintier, Cailletaud and Piques (2006).
We’ve done our own validation experiments. My PhD dissertation (University of Toledo, 2001) contains an extensive database of tension/torsion/compression fatigue tests against which our critical plane algorithms were validated. Two additional PhD dissertations that I co-advised generated additional validations. Dr. Malik Ait Bachir’s thesis (2010) validated mathematically that the scaling law we use for small cracks is valid across all multiaxial loading states. Dr. Ryan Harbour’s thesis (2006) contains a database of multiaxial, variable amplitude fatigue experiments against which our rainflow and damage accumulation procedures were extensively validated.
Validation from partners. We partner with several testing labs. We have invested in testing protocols that produce clean, accurate data and we have run validation programs with our partners to verify the effectiveness of our testing protocols. We’ve demonstrated significant improvements to test efficiency and reproducibility (Goosens and Mars 2018) and (Mars and Isasi 2019). We’ve validated techniques for estimating precursor size and size distribution (Robertson et al 2020, Li et al 2015).
Validation from users. Three (3) of the top 12 tire companies and six (6) of the top 10 global non-tire rubber companies now use our solutions. Most of our users have run internal validation programs to show the effectiveness of our solutions for their applications. Most of these studies are unpublished, but the fact that our user base has continued growing at ~20%/year for 12 years (as of this year) says something important both about the technical validation case and the business validation case. Validation studies have been published with the US Army (Mars, Castanier, Ostberg 2017), GM (Barbash and Mars 2016), Tenneco (Goossens et al 2017) and Caterpillar (Ramachandran et al 2017).
Validation from external groups. There are several academic groups that have independently applied and validated components of our approach. There are too many to list completely, but a few recent examples include Zarrin-Ghalami et al (2020), Belkhira et al (2020) and Tobajas et al (2020).
Software verification, benchmarking and unit testing. In addition to the experimental validations mentioned above, each time we build a new version of our software, we execute a series of automated tests. These tests verify every line of code against expected function, and they ensure that as we add new features, we do not introduce unintended changes. The benchmarks include tests that verify things like coordinate frame objectivity (rigid rotations under static load should do no damage and the same strain history written in two different coordinate systems should have the same life), and check known results pertaining to material models and cycle counting rules. You can read more about our software quality processes here.
It is safe to say that no other solution for fatigue life prediction of rubber has been tested and validated against a larger number of applications than Endurica’s.
References
Aıt-Bachir, M. “Prediction of crack initiation in elastomers in the framework of Configurational Mechanics.” PhD diss., Ph. D. thesis, Ecole Centrale de Nantes, Nantes (France), 2010.
Barbash, Kevin P., and William V. Mars. Critical plane analysis of rubber bushing durability under road loads. No. 2016-01-0393. SAE Technical Paper, 2016.
Belkhiria, Salma, Adel Hamdi, and Raouf Fathallah. “Cracking energy density for rubber materials: Computation and implementation in multiaxial fatigue design.” Polymer Engineering & Science (2020).
Cadwell, S. M., R. A. Merrill, C. M. Sloman, and F. L. Yost. “Dynamic fatigue life of rubber.” Rubber Chemistry and Technology 13, no. 2 (1940): 304-315.
Choi, I. S., and C. M. Roland. “Intrinsic defects and the failure properties of cis-1, 4-polyisoprenes.” Rubber chemistry and technology 69, no. 4 (1996): 591-599.
Fielding, J. H. “Flex life and crystallization of synthetic rubber.” Industrial & Engineering Chemistry 35, no. 12 (1943): 1259-1261.
Goossens, J.R., Mars, W., Smith, G., Heil, P., Braddock, S. and Pilarski, J., 2017. Durability Analysis of 3-Axis Input to Elastomeric Front Lower Control Arm Vertical Ride Bushing (No. 2017-01-1857). SAE Technical Paper. https://doi.org/10.4271/2017-01-1857
Goossens, Joshua R., and William V. Mars. “Finitely Scoped, High Reliability Fatigue Crack Growth Measurements.” Rubber Chemistry and Technology 91, no. 4 (2018): 644-650. https://doi.org/10.5254/rct.18.81532
Harbour, Ryan Joseph. Multiaxial deformation and fatigue of rubber under variable amplitude loading. Vol. 67, no. 12. 2006.
Harbour, Ryan J., Ali Fatemi, and Will V. Mars. “Fatigue crack orientation in NR and SBR under variable amplitude and multiaxial loading conditions.” Journal of materials science 43, no. 6 (2008): 1783-1794.
Huneau, Bertrand, Isaure Masquelier, Yann Marco, Vincent Le Saux, Simon Noizet, Clémentine Schiel, and Pierre Charrier. “Fatigue crack initiation in a carbon black–filled natural rubber.” Rubber Chemistry and Technology 89, no. 1 (2016): 126-141.
Lake, G. J., and P. B. Lindley. “Cut growth and fatigue of rubbers. II. Experiments on a noncrystallizing rubber.” Journal of Applied Polymer Science 8, no. 2 (1964): 707-721.
Li, Fanzhu, Jinpeng Liu, W. V. Mars, Tung W. Chan, Yonglai Lu, Haibo Yang, and Liqun Zhang. “Crack precursor size for natural rubber inferred from relaxing and non-relaxing fatigue experiments.” International Journal of Fatigue 80 (2015): 50-57.
Mars, William Vernon. Multiaxial fatigue of rubber. 2001.
Mars, Will V. “Cracking energy density as a predictor of fatigue life under multiaxial conditions.” Rubber chemistry and technology 75, no. 1 (2002): 1-17.
Mars, W. V., and A. Fatemi. “Analysis of fatigue life under complex loading: Revisiting Cadwell, Merrill, Sloman, and Yost.” Rubber chemistry and technology 79, no. 4 (2006): 589-601.
Mars, W. V., and A. Fatemi. “Nucleation and growth of small fatigue cracks in filled natural rubber under multiaxial loading.” Journal of materials science 41, no. 22 (2006): 7324-7332.
Mars, W. V. “Computed dependence of rubber’s fatigue behavior on strain crystallization.” Rubber Chemistry and Technology 82, no. 1 (2009): 51-61. https://doi.org/10.5254/1.3557006
Mars, William V., Matthew Castanier, David Ostberg, and William Bradford. “Digital Twin for Tank Track Elastomers: Predicting Self-Heating and Durability.” In Proceedings of the 2017 Ground Vehicle Systems Engineering and Technology Symposium (GVSETS). 2017.pdf here
Mars, W. V., and M. Isasi. “Finitely scoped procedure for generating fully relaxing strain-life curves.” In Constitutive Models for Rubber XI: Proceedings of the 11th European Conference on Constitutive Models for Rubber (ECCMR 2019), June 25-27, 2019, Nantes, France, p. 435. CRC Press, 2019.
Muhr, A. H. “Modeling the stress-strain behavior of rubber.” Rubber chemistry and technology 78, no. 3 (2005): 391-425.Lake and Thomas 1967
Ramachandran, Anantharaman, Ross P. Wietharn, Sunil I. Mathew, W. V. Mars, and M. A. Bauman. “Critical Plane Selection Under Nonrelaxing Simple Tension with Strain Crystallization.” In Fall 192nd Technical Meeting of the Rubber Division, pp. 10-12. 2017.
Rivlin, R. S., and A. G. Thomas. “Rupture of rubber. I. Characteristic energy for tearing.” Journal of polymer science 10, no. 3 (1953): 291-318.Gent, Lindley and Thomas, 1964
Roberts, B. J., and J. B. Benzies. “The relationship between uniaxial and equibiaxial fatigue in gum and carbon black filled vulcanizates.” Proceedings of rubbercon 77, no. 2 (1977): 1-13.
Robertson, Christopher G., Lewis B. Tunnicliffe, Lawrence Maciag, Mark A. Bauman, Kurt Miller, Charles R. Herd, and William V. Mars. “Characterizing Distributions of Tensile Strength and Crack Precursor Size to Evaluate Filler Dispersion Effects and Reliability of Rubber.” Polymers 12, no. 1 (2020): 203. Pdf here
Saintier, Nicolas, Georges Cailletaud, and Roland Piques. “Multiaxial fatigue life prediction for a natural rubber.” International Journal of Fatigue 28, no. 5-6 (2006): 530-539.
Tobajas, Rafael, Daniel Elduque, Elena Ibarz, Carlos Javierre, and Luis Gracia. “A New Multiparameter Model for Multiaxial Fatigue Life Prediction of Rubber Materials.” Polymers 12, no. 5 (2020): 1194.
Zarrin-Ghalami, Touhid, Sandip Datta, Robert Bodombo Keinti, and Ravish Chandrashekar. Elastomeric Component Fatigue Analysis: Rubber Fatigue Prediction and Correlation Comparing Crack Initiation and Crack Growth Methodologies. No. 2020-01-0193. SAE Technical Paper, 2020.




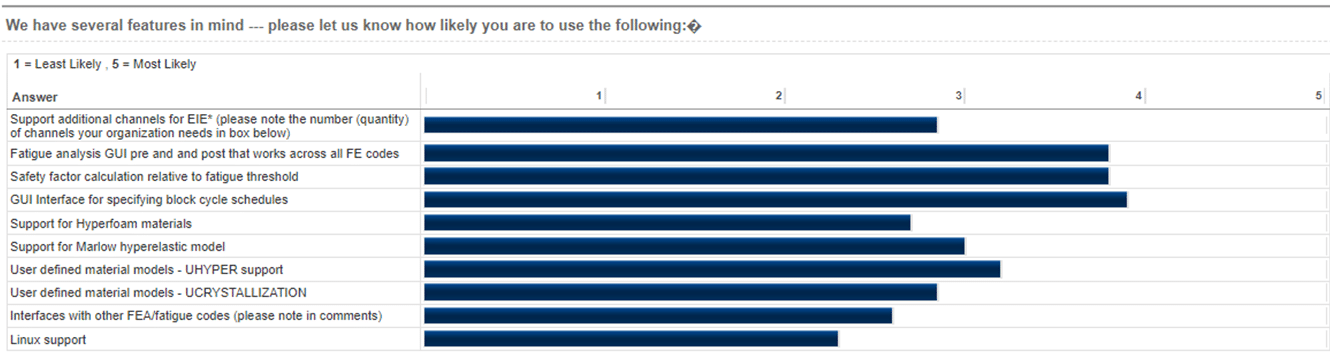
 Once a year, we ask our users to weigh in on what we can do to further improve your experiences with the Endurica fatigue solvers. The feedback helps us aim our development at bringing you winning capabilities. It is also a marker we can use to gauge progress.
Once a year, we ask our users to weigh in on what we can do to further improve your experiences with the Endurica fatigue solvers. The feedback helps us aim our development at bringing you winning capabilities. It is also a marker we can use to gauge progress.


 The Tire Society held its 40th annual meeting last month with the theme The Virtual Tire. It has always been the place to see up and coming ideas, to see who is pushing into the frontiers of the field, and to renew professional connections across the industry. Endurica was very proud to sponsor this year.
The Tire Society held its 40th annual meeting last month with the theme The Virtual Tire. It has always been the place to see up and coming ideas, to see who is pushing into the frontiers of the field, and to renew professional connections across the industry. Endurica was very proud to sponsor this year. GM’s Mike Anderson, Executive Director of Global Virtual Design, Development and Validation, kicked off the meeting with his keynote lecture, titled “The Move To Virtual”. He spoke of GM’s target to achieve 100% virtual design by 2025. Anderson explained that this doesn’t mean that physical testing will go away, but rather that GM is dead serious about getting to a “right the first time” scenario rather than a “discover and recover” mode. “It’s a measure twice, cut once” culture, he said. He noted that upstart competitors are sprinting ahead in areas like EVs through the use of simulation and that the speed of discovery has increased significantly in the current competitive environment. Simulation drives learning speed, not only because of the opportunity to get engineering answers at the pre-build phase but also because it enables exploration of more of the design space and more of the performance outcomes. He told the conference that “we need to go beyond just replicating physical tests with simulation, we need to leverage the strength of simulation to go beyond test”. In the Q&A, Anderson was asked whether suppliers will also be expected to be virtual. “That’s gonna be tough to play together” for rubber part suppliers that can’t engage via simulation.
GM’s Mike Anderson, Executive Director of Global Virtual Design, Development and Validation, kicked off the meeting with his keynote lecture, titled “The Move To Virtual”. He spoke of GM’s target to achieve 100% virtual design by 2025. Anderson explained that this doesn’t mean that physical testing will go away, but rather that GM is dead serious about getting to a “right the first time” scenario rather than a “discover and recover” mode. “It’s a measure twice, cut once” culture, he said. He noted that upstart competitors are sprinting ahead in areas like EVs through the use of simulation and that the speed of discovery has increased significantly in the current competitive environment. Simulation drives learning speed, not only because of the opportunity to get engineering answers at the pre-build phase but also because it enables exploration of more of the design space and more of the performance outcomes. He told the conference that “we need to go beyond just replicating physical tests with simulation, we need to leverage the strength of simulation to go beyond test”. In the Q&A, Anderson was asked whether suppliers will also be expected to be virtual. “That’s gonna be tough to play together” for rubber part suppliers that can’t engage via simulation. Pooya Behroozinia of Maxxis Tires spoke on “Tire Durability Prediction Using Three-Element Layered Mesh for Cord-Rubber Composites”. Behroozinia shared a tire meshing technique for improving representation of interlaminar shearing in their tire model. They used Endurica DT to simulate the damage accruing across all of the 6 steps in a stepped-up load durability test, and they were able to predict correctly the lower sidewall failure mode, the life (45 hours observed, 38 hours predicted), and the crack orientation. They also had a 2nd validation case in which the loads were increased by 10% in all steps of the test. The simulation again predicted correct failure, and the comparison of experimental life (41000 km) to simulated life (36330 km) was in good agreement.
Pooya Behroozinia of Maxxis Tires spoke on “Tire Durability Prediction Using Three-Element Layered Mesh for Cord-Rubber Composites”. Behroozinia shared a tire meshing technique for improving representation of interlaminar shearing in their tire model. They used Endurica DT to simulate the damage accruing across all of the 6 steps in a stepped-up load durability test, and they were able to predict correctly the lower sidewall failure mode, the life (45 hours observed, 38 hours predicted), and the crack orientation. They also had a 2nd validation case in which the loads were increased by 10% in all steps of the test. The simulation again predicted correct failure, and the comparison of experimental life (41000 km) to simulated life (36330 km) was in good agreement. Vidit Bansal of CEAT spoke on “Incremental, Critical Plane Analysis and Experimental Verification for TBR Tyre Bead Endurance Applications”. Similar to the Maxxis paper, CEAT used Endurica DT to simulate a multi-step durability test with loads ranging from 80% to 250%. In this paper, two different truck tire sizes were modeled and tested, a 10.00R20 and an 11.00R20. The analysis correctly predicted the ply turnup as the critical location. The predicted lives of the two tire sizes were predicted at 90-93% of the actual tested life in both cases.
Vidit Bansal of CEAT spoke on “Incremental, Critical Plane Analysis and Experimental Verification for TBR Tyre Bead Endurance Applications”. Similar to the Maxxis paper, CEAT used Endurica DT to simulate a multi-step durability test with loads ranging from 80% to 250%. In this paper, two different truck tire sizes were modeled and tested, a 10.00R20 and an 11.00R20. The analysis correctly predicted the ply turnup as the critical location. The predicted lives of the two tire sizes were predicted at 90-93% of the actual tested life in both cases. Tom Ebbott and Gobi Gobinath of Goodyear spoke on “A Model for Predicting Residual Casing Life of a Tire Following an Impact Event”. This work demonstrated the consequences on tire damage development of a range of impact event scenarios (3 speeds, 4 impact angles, 3 different wear states) early in the life of the tire. It used Endurica DT to accrue damage from both the impact event (computed with explicit FEA) and subsequent tire runout under steady state rolling conditions (computed with implicit FEA). The crack growth rate curve during the impact was based upon experimental measurements of the critical tearing energy at impact rates. When asked about experimental validation of the simulation results during the Q&A, Ebbott noted that “the modeling work stands on its own – it is based on sound physics”.
Tom Ebbott and Gobi Gobinath of Goodyear spoke on “A Model for Predicting Residual Casing Life of a Tire Following an Impact Event”. This work demonstrated the consequences on tire damage development of a range of impact event scenarios (3 speeds, 4 impact angles, 3 different wear states) early in the life of the tire. It used Endurica DT to accrue damage from both the impact event (computed with explicit FEA) and subsequent tire runout under steady state rolling conditions (computed with implicit FEA). The crack growth rate curve during the impact was based upon experimental measurements of the critical tearing energy at impact rates. When asked about experimental validation of the simulation results during the Q&A, Ebbott noted that “the modeling work stands on its own – it is based on sound physics”. These days everybody’s talking about whether to meet in person or online. There are great tools available for online meetings, and these have helped us navigate Covid-19. Like everyone else, Endurica teammates regularly use online meeting technology. But if there is one thing we learned over the last year, it is that sometimes physical presence really matters. Living and working in isolation is just not healthy in the long run.
These days everybody’s talking about whether to meet in person or online. There are great tools available for online meetings, and these have helped us navigate Covid-19. Like everyone else, Endurica teammates regularly use online meeting technology. But if there is one thing we learned over the last year, it is that sometimes physical presence really matters. Living and working in isolation is just not healthy in the long run.